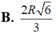
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Ta có O H = I O . tan 30 0 = R 3 ⇒ H A = O A 2 − O H 2 = R 6 3 .
Vậy A B = 2 R 6 3
Đáp án C
Phương pháp:
+) Chứng minh mặt phẳng (P) không cắt đáy (O';R)
+) Tìm phần hình chiếu của mặt phẳng (P) trên mặt đáy. Tính S h c
+) Sử dụng công thức S h c = S . cos 60
Cách giải:
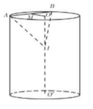
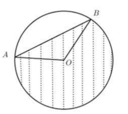
Gọi M là trung điểm của AB ta có:
O M = O A 2 − A B 2 2 = R 2 − 3 R 2 4 = R 2
Giả sử mặt phẳng (P) cắt trục OO’ tại I. Ta có : IA = IB nên Δ I A B cân tại I, do đó M I ⊥ A B
Vậy diện tích phần thiết diện cần tìm là :
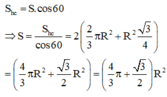
Đáp án D
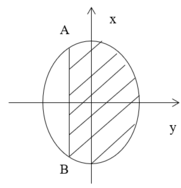
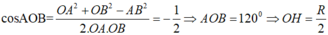
Chọn hệ trục tọa độ như hình vẽ ⇒ pt đường tròn đáy là:
Hình chiếu của phần elip xuống đáy là miền gạch chéo như hình vẽ
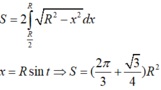
Gọi diện tích phần elip cần tính là S’. theo công thức hình chiếu ta có
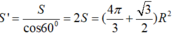
Đáp án D
cos A O B ^ = O A 2 + O B 2 - A B 2 2 . O A . O B = - 1 2 ⇒ A O B ^ = 120 0 ⇒ O H = R 2
Chọn hệ trục tọa độ như hình vẽ pt đường tròn đáy là:
x 2 + y 2 = R 2 ⇔ y = ± R 2 - x 2
Hình chiếu của phần elip xuống đáy là miền gạch chéo như hình vẽ
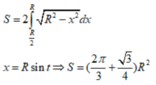
Gọi diện tích phần elip cần tính là S’. theo công thức hình chiếu ta có
S ' = S cos 60 0 = 2 S = ( 4 π 3 + 3 2 ) R 2
