Từ các chữ số thuộc tập X = {0;1;2;3;4;5;6;7} có thể lập được bao nhiêu số tự nhiên gồm 6 chữ số khác nhau sao cho mỗi số tự nhiên đó đều chia hết cho 18.
A. 720.
B. 860.
C. 984.
D. 1228.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số các số thuộc tập S là 7.8.8=448. Số rút ra thoả mãn có dạng
A
B
C
¯
với ![]()
![]() Mỗi cách chọn ra bộ ba số thuộc tập {1,...,9} thu được một bộ số (a; b+1; c+2) tương ứng với một bộ ba số (a;b;c) và cho ta một số có ba chữ số thoả mãn yêu cầu bài toán. Vậy có tất cả
C
9
3
số thoả mãn. Xác suất cần tính bằng
Mỗi cách chọn ra bộ ba số thuộc tập {1,...,9} thu được một bộ số (a; b+1; c+2) tương ứng với một bộ ba số (a;b;c) và cho ta một số có ba chữ số thoả mãn yêu cầu bài toán. Vậy có tất cả
C
9
3
số thoả mãn. Xác suất cần tính bằng 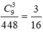
Chọn đáp án C.

Có \(A_8^5=6720\) số bất kì (kể cả bắt đầu bằng 0)
Do vai trò của các chữ số là như nhau, nên ở mỗi vị trí, mỗi chữ số xuất hiện: \(67220:5=1344\) lần
Ta chọn 1 số làm đại diện tính toán, ví dụ số 3, do số 3 xuất hiện ở các hàng chục ngàn, ngàn, trăm, chục, đơn vị mỗi hàng đều 1344 lần nên tổng giá trị của số 3 là:
\(1344.\left(3.10000+3.1000+3.100+3.10+3.1\right)=1344.11111.3\)
Do vai trò các chữ số là giống nhau nên tổng các chữ số là:
\(S_1=1344.11111.\left(0+3+4+5+6+7+8+9\right)\)
Bây giờ ta lập các số có số 0 đứng đầu, nó đồng nghĩa với việc lập số có 4 chữ số từ các chữ số 3,4,5,6,7,8
Số số lập được là: \(A_7^4=840\) số
Do vai trò các chữ số như nhau nên mỗi vị trí mỗi chữ số xuất hiện \(840:4=210\) lần
Tương tự như trên, ta có tổng trong trường hợp này là:
\(S_2=210.1111.\left(3+4+5+6+7+8+9\right)\)
Giờ lấy \(S_1-S_2\) là được

Chọn C
Gọi số cần tìm là a = a 1 a 2 a 3 a 4 a 5 ¯ a i ≠ 0 Do a ⋮ 3 nên a 1 + a 2 + a 3 + a 4 + a 5 ⋮ 3
Nếu a 1 + a 2 + a 3 + a 4 ⋮ thì a 5 = 0 hoặc a 5 = 3
Nếu a 1 + a 2 + a 3 + a 4 chia 3 dư 1 thì a 5 = 2 hoặc a 5 = 5 .
Nếu a 1 + a 2 + a 3 + a 4 chia 3 dư 2 thì a 5 = 1 hoặc a 5 = 4 .
Như vậy, từ một số có 4 chữ số a 1 a 2 a 3 a 4 (các số được lấy từ tập A) sẽ tạo được 2 số tự nhiên có 5 chữ số thỏa mãn yêu cầu bài toán.
Dễ thấy từ các chữ số của tập A có thể lập được 5.6.6.6 = 1080 số tự nhiên có 4 chữ số.
Do đó từ các chữ số của tập A sẽ lập được 2.1080 = 2160 số chia hết cho 3 có 5 chữ số.

1) Các số thỏa mãn là 59; 68; => có 2 chữ số thỏa mãn
2) X = {1;2;3} ; {1;2;4}; {1;2;5} ; {1;2;3;4} ; {1;2;3;5}; {1;2;3;4;5}
3) Số có chữ số hàng chục là 1, có 12;13;...; 19 => có 8 số
Số có chữ số hàng chục là 2 gồm : 23;24;...; 29 => có 7 số
Số có chữ số hàng chục là 3 gồm 34;35;...;39 => có 6 số
Số có chữ số hàng chục là 4 gồm 45; 46;...49 => có 5 số
Số có chữ số hàng chục là 5 gồm 56;57;...;59 => có 4 số
Số có chữ số hàng chục là 6 gồm: 67; 68; 69 => có 3 số
tương tự; có số 78; 79; 89 => có 3 số
Vậy số phân tử của X là: 8 + 7 + 6 + 5 + ...+ 2 + 1 = 36
4) có 4 tâp hợp , đó là {1;2}; {1; 4}; {3;2}; {3; 4}
5) tập S có 3 phần tử => có 23 = 8 tập hợp con
Công thức tổng quat: số tập hợp con của tập n phần tử là 2n

a) A = { 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 }
B = { 2 ; 4 ; 6 ; 8 }
b) C = { 0 ; 1 ; 3 ; 5 ; 7 ; 9 }
Học tốt #
a) A = { 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 }
B = { 2 ; 4 ; 6 ; 8 }
b) C = { 0 ; 1 ; 3 ; 5 ; 7 ; 9 }
Chọn C
Giả sử số lập được có dạng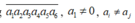
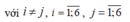
Ta có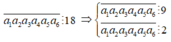
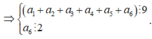
Vì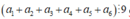 nên ta có các trường hợp sau
nên ta có các trường hợp sau
Trường hợp 1: a 1 , a 2 , a 3 , a 4 , a 5 , a 6 được chọn từ
+ Có 3 cách chọn chọn a 6
+ Có 5! cách chọn chọn bộ 5 số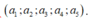
Suy ra có 3.5! = 360 số.
Trường hợp 2: a 1 , a 2 , a 3 , a 4 , a 5 , a 6 được chọn từ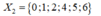
+ a 6 = 0, có 5! cách chọn bộ 5 số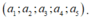
+ a 6 ≠ 0 khi đó a 6 có 3 cách chọn, a 1 có 4 cách chọn và có 4! cách chọn bộ 4 số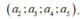
Suy ra có 5! + 3.4.4!= 408 số
Trường hợp 3: a 1 , a 2 , a 3 , a 4 , a 5 , a 6 được chọn từ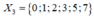
+ a 6 = 0, có 5! cách chọn bộ 5 số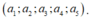
+ a 6 ≠ 0 khi đó a 6 có 1 cách chọn, a 1 có 4 cách chọn và có 4! cách chọn bộ 4 số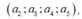
Suy ra có 5! + 1.4.4! = 216 số
Vậy có: 360 + 408 + 216 = 984 số.