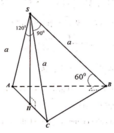
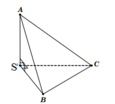
Cho khối chóp S.ABC có SA = SB = SC =a, A S B ^ = 60 o , B S C ^ = 90 o , C S A ^ = 120 o Gọi M,N lần lượt là các điểm trên cạnh AB và SC sao cho C N S C = A M A B Khi khoảng cách giữa M và N nhỏ nhất, tính thể tích V của khối chóp S.AMN.
A. V = 2 a 3 72
B. V = 5 2 a 3 72
C. V = 5 2 a 3 432
D. V = 2 a 3 432

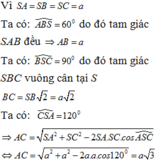


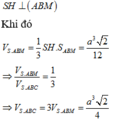
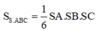

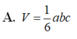
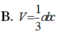
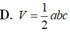
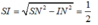
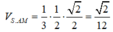
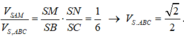
Đáp án C
Ta có thể tích khối chóp S.ABC là
Theo đẳng thức trên ta có biểu diễn véctơ
Do đó
Dấu bằng đạt tại