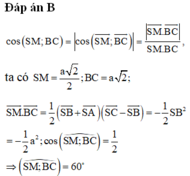
Đáp án B

c os S M ; B C = c os S M → ; B C → = S M → . B C → S M . B C , ta có   S M = a 2 2 ; B C = a 2 ;

S M → . B C → = 1 2 S B → + S A → S C → − S B → = − 1 2 S B 2 = − 1 2 a 2 ;   c os S M ; B C ^ = 1 2 ⇒ S M ; B C ^ = 60 ∘

Chọn A.

Chọn C

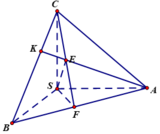
Trong tam giác ABC kẻ đường cao AK và CF và  nên E là trực tâm tam giác ABC.

Ta có:

Ta có CE là hình chiếu của SC lên mặt phẳng (ABC).

Ta có tam giác SCF vuông tại S nên

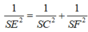
Mặt khác tam giác SAB vuông tại S nên:

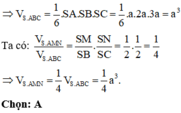
Phương pháp:

+) Thể tích của tứ diện vuông có độ dài các cạnh góc vuông là a, b, c là:  V = 1 6 a b c

+) Sử dụng công thức tỉ số thể tích Simpson

Cách giải:

S.ABC là tứ diện vuông tại đỉnh S 

a: \(\widehat{SB;AB}=\widehat{SBA}\)

SA\(\perp\)(ABC)

=>\(SA\perp AB;SA\perp AC;SA\perp BC\)

Xét ΔSAB vuông tại A có \(tanSBA=\dfrac{SA}{AB}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)

=>\(\widehat{SBA}=60^0\)

=>\(\widehat{SB;AB}=60^0\)

b:

\(\widehat{SC;AC}=\widehat{SCA}\)

Xét ΔSAC vuông tại A có \(tanSCA=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)

nên \(\widehat{SCA}=60^0\)

=>\(\widehat{SC;AC}=60^0\)

c: ΔABC đều có AM là đường trung tuyến

nên \(AM=BC\cdot\dfrac{\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\)

Ta có: SA\(\perp\)(ABC)

AM\(\subset\)(ABC)

Do đó: SA\(\perp\)AM

=>ΔSAM vuông tại A

\(\widehat{SM;AM}=\widehat{SMA}\)

Xét ΔSMA vuông tại A có \(tanSMA=\dfrac{SA}{AM}=\dfrac{a\sqrt{3}}{\dfrac{a\sqrt{3}}{2}}=2\)

=>\(\widehat{SMA}\simeq63^026'\)

=>\(\widehat{SM;AM}\simeq63^026'\)

a.

Góc giữa SB và AB là góc \(\widehat{SBA}\)

Trong tam giác vuông SAB:

\(tan\widehat{SBA}=\dfrac{SA}{AB}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)

\(\Rightarrow\widehat{SBA}=60^0\)

b.

Góc giữa SC và AC là góc \(\widehat{SCA}\)

\(tan\widehat{SCA}=\dfrac{SA}{AC}=\sqrt{3}\Rightarrow\widehat{SCA}=60^0\)

c.

Góc giữa SM và AM là góc \(\widehat{SMA}\)

AM là trung tuyến tam giác đều \(\Rightarrow AM=\dfrac{a\sqrt{3}}{2}\)

\(\Rightarrow tan\widehat{SMA}=\dfrac{AM}{SA}=2\Rightarrow\widehat{SMA}=60^026'\)

Chọn A       

Chọn hệ trục tọa độ A(1;0;0), B(0;2;0), C(0;0;3).

Khi đó M thuộc mặt phẳng (ABC) thỏa mãn đề bài nên  S M = 6 3 11

có 

 Gắn vào hệ trục Oxyz có 

CÓ : S(0,0,0) A(0,0,a) , B(0,a,0), C(a,0,0)

e nhớ ko lầm là a đã học tới bài này âu mà sao bik làm hay z???