BC = \(\sqrt{3^2+4^2}\) = 5

Tam giác ABC vuông tại A => Trung tuyến AM = BC/2 = 5/2 cm

AG = 2AM/3 = 2/3 x 5/2 = 5/3 cm

Tham khảo tại đây:

https://olm.vn/hoi-dap/detail/4163827016.html

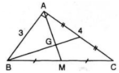
ΔABC vuông tại A có BC2 = AB2 + AC2 (định lí Pitago)

⇒ BC2 = 32 + 42 = 25 ⇒ BC = 5 (cm)

Gọi M là trung điểm của BC ⇒ AM là trung tuyến.

Vì theo đề bài: trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên

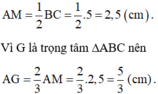
tự vẽ hình ta vẽ AK là đường trung tuyến của cạnh huyền

xét tam giác ABC có:

AB²+AC² = BC² ( đ/lý py-ta-go)

=> 3² + 4² = BC²

=>   9  + 16  = BC²

=> BC = 25

=> BC = \(\sqrt{25}=5cm\)

tam giác ABC có AK là đường trung tuyến vs cạnh huyền => AK = \(\frac{BC}{2}=\frac{5}{2}=2,5\)

=> AG = \(\frac{2}{3}AK\) (đ/lý) => \(\frac{2}{3}x2,5=1,66666667\)

hình như mk làm sai hoặc bn sai đề

để ghi lại khúc cuối

AG = \(\frac{2}{3}AK=>\frac{2}{3}x\frac{5}{2}=\frac{5}{3}cm\)

có \(5:2=\frac{5}{2}\) nên mới có 5/2

Gọi D là trung điểm BC; E là trung điểm AC

Trong tam giác ABC có BC² = AB² + AC² = 3² + 4² = 25

=> BC = 5

Trong tam giác vuông ABC có AD là đường trung tuyến ứng với cạnh huyền BC nên AD = BD = CD

mà BD = CD = BC/2 = 5/2 = 2,5 nên AD = 2,5

Ta có AG/AD = 2/3 => AG = (AD.2)/3 = (2,5 x 2)/3 = 5/3

∆ABC vuông tại A => BC² = AB² + AC²

BC² = 3² + 4²

BC² = 25

BC = 5

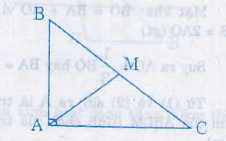
Gọi M là trung điểm của BC => AM là trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên AM = $\frac{1}{2}$ BC

Vì G là trọng tâm của ∆ ABC nên AG =$\frac{2}{3}$ AM => AG =$\frac{2}{3}$.$\frac{1}{2}$ BC

=> AG = $\frac{1}{3}$ BC = $\frac{1}{3}$ .5 = 1.7cm

Gọi D là trung điểm BC; E là trung điểm AC
Trong tam giác ABC có BC2 = AB2 + AC2 = 32 + 42 = 25
=> BC = 5
Trong tam giác vuông ABC có AD là đường trung tuyến ứng với cạnh huyền BC nên AD = BD = CD
mà BD = CD = BC/2 = 5/2 = 2,5 nên AD = 2,5
Ta có AG/AD = 2/3 => AG = (AD.2)/3 = (2,5 x 2)/3 = 5/3