Tính tổng
S
=
C
2018
1009
+
C
2018
1010
+
C
2018
1011
+
...
+
C
2018
2018
(trong tổng đó, các số hạng có dạng
C
2018
k
với k nguyên dương nhận giá trị liên tục từ 1009 đến 2018 ). A.
S
=
2
2018
−
C
2018
1009
B.
S
=
2
2017
+
1
2
C
2018
1009
C....
Đọc tiếp
Tính tổng S = C 2018 1009 + C 2018 1010 + C 2018 1011 + ... + C 2018 2018 (trong tổng đó, các số hạng có dạng C 2018 k với k nguyên dương nhận giá trị liên tục từ 1009 đến 2018 ).
A. S = 2 2018 − C 2018 1009
B. S = 2 2017 + 1 2 C 2018 1009
C. S = 2 2017 − 1 2 C 2018 1009
D. S = 2 2017 − C 2018 1009
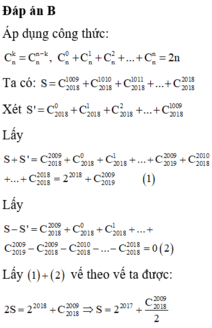
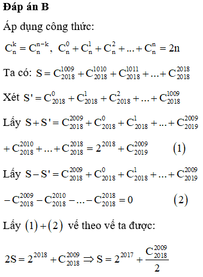
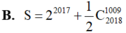
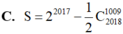
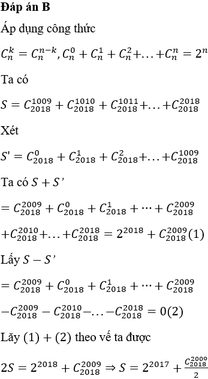
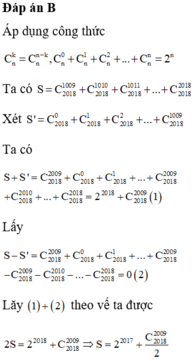
Đáp án B
Ta có 1 + x 2018 = ∑ k = 0 2018 C 2018 k x k = C 2018 0 + C 2018 1 x + ... + C 2018 2018 x 2018 .
Chọn x = 1 ⇒ 2 2018 = C 2018 0 + C 2018 1 + ... + C 2018 2018 .
Vì C n k = C n n − k ⇒ 2 2018 = 2 C 2018 1010 + C 2018 1011 + C 2018 2018 + C 2018 1009 = 2 S + C 2018 1009 ⇒ S = 2 2017 + 1 2 C 2018 1009 .