Giải hộ em câu 10,11,13 và 15 ạ!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


8:
\(=\dfrac{cos10-\sqrt{3}\cdot sin10}{sin10\cdot cos10}=\dfrac{2\left(\dfrac{1}{2}\cdot cos10-\dfrac{\sqrt{3}}{2}\cdot sin10\right)}{sin20}=\dfrac{sin\left(30-10\right)}{sin20}=1\)
10:
\(=\left(2-\sqrt{3}\right)^2+\left(2+\sqrt{3}\right)^2\)
=7-4căn 3+7+4căn 3=14
12:
\(=cos^270^0+\dfrac{1}{2}\left[cos60-cos140\right]\)
\(=cos^270^0+\dfrac{1}{2}\cdot\dfrac{1}{2}-\dfrac{1}{2}\cdot2cos^270^0+\dfrac{1}{.2}\)
=1/4+1/2=3/4

1. D (trọng âm rơi vào âm 2, còn lại âm 1) 2. B (âm 2, còn lại âm 1)
3. A (âm 3, còn lại âm 1) 4. C (âm 1, còn lại âm 2) 5. B (âm 2, còn lại âm 1)
6. A (âm 2, còn lại âm 1) 7. B (âm 3, còn lại âm 1)
từ câu 8 - 10 hợp lý hơn nếu là bài chọn từ có phần phát âm khác:
8. D (nếu phần gạch chân là chữ i)
9. B (nếu phần gạch chân là ea)
10. C (nếu phần gạch chân là chữ e; riêng câu này nếu đúng đề bài là chọn từ có trọng âm khác, thì đáp án cũng là C nhé, C âm 1, còn lại âm 2)


1.1
Pt có 2 nghiệm trái dấu và tổng 2 nghiệm bằng -3 khi:
\(\left\{{}\begin{matrix}ac< 0\\x_1+x_2=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\left(m+2\right)< 0\\\dfrac{2m+1}{m+2}=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -2\\m=-\dfrac{7}{5}\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn
b.
Pt có nghiệm kép khi:
\(\left\{{}\begin{matrix}m+2\ne0\\\Delta=\left(2m+1\right)^2-8\left(m+2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-2\\4m^2-4m-15=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=\dfrac{5}{2}\\m=-\dfrac{3}{2}\end{matrix}\right.\)

Bạn ko đưa ngữ liệu, đưa ngang như v ai hiểu gì đâu
Bạn học sách mới mà.

5.
\(\Delta=\left(-2\right)^2-4\left(-15\right)=64\)
6.
\(\Delta'=2^2-5.\left(-7\right)=39\)
Mà thầy ơi em hok hiểu khúc đầu làm sao để ra cái đó ròi ra kết quả á :((( cả 2 câu lun

a: góc OBA+góc OCA=90+90=180 độ
=>ABOC nội tiếp
b: góc OIE=góc OCE=90 độ
=>OICE là tứ giác nội tiếp
=>góc OEI=góc OCI
=>góc OEI=góc OCB
OBAC nội tiếp
=>góc OCB=góc OAB
=>góc OEI=góc OAB
=>góc OEI=góc OAI
=>OIAE nội tiếp

x2-(m-1)x+m-2=0(1)
Để phương trình có hai nghiệm phân biệt thì Δ=(-m+1)2-4(m-2)
=m2-2m+1-4m+8
=m2-6m+9
=(m-3)2≥0 với mọi m
⇒phương trình luôn có hai nghiệm phân biệt
Áp dụng định lý Vi-ét ta có:\(\begin{cases} x_1+x_2=m-2 \\ x_1.x_2=m-1 \end{cases}\)(2)
TH1:x1,x2 là hai cạnh góc vuông
⇒x1=x2
Từ (2)\(\begin{cases} x_1+x_1=m-2 \\ x_1^2=m-1 \end{cases}\)
\(\Leftrightarrow\)\(\begin{cases} x_1=\frac{m-1}{2}\\ x_1=\sqrt{m-2} \end{cases}\)
\(\Leftrightarrow\)\(\dfrac{m-1}{2}\)=\(\sqrt{m-2}\)
\(\Leftrightarrow\)\(\dfrac{m^2-2m+1}{4}\)=m-2
\(\Leftrightarrow\)m2-6m+9=0
\(\Leftrightarrow\)(m-3)2=0
\(\Leftrightarrow\)m=3
TH2:x1 là cạnh huyền,x2 là cạnh góc vuông
⇒x1=\(\sqrt{2}\)x2
Từ (2)⇒\(\begin{cases} \sqrt{2} x_2+x_2=m-1 \\ \sqrt{2} x_2^2=m-2 \end{cases}\)
\(\Leftrightarrow\)\(\begin{cases} x_2= \frac{m-1}{1+\sqrt{2}} \\ x_2=\sqrt{\frac{m-2}{\sqrt{2}}} \end{cases}\)
\(\Leftrightarrow\)\(\dfrac{m-1}{1+\sqrt{2}}\)=\(\sqrt{\dfrac{m-2}{\sqrt{2}}}\)
\(\Leftrightarrow\)\(\dfrac{m^2-2m+1}{3+2\sqrt{2}}\)=\(\dfrac{m-2}{\sqrt{2}}\)
\(\Leftrightarrow\)\(\left(3+2\sqrt{2}\right)\)\(m\)\(-6-2\sqrt{2}\)\(=\sqrt{2}m^2-2\sqrt{2}m+\sqrt{2}\)
\(\Leftrightarrow\sqrt{2}m^2-\left(4\sqrt{2}+3\right)m+3\sqrt{2}+6=0\)
\(\Leftrightarrow\)rồi m bằng bao nhiêu thì tự giải nhé mệt r






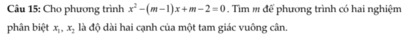
Câu 14:
const R=2;