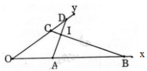
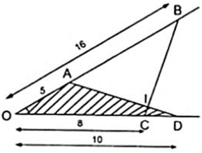
trên một cạnh của góc XOY, đặt các đoạn thẳng OA = 5 cm, OB =16 cm. trên cạnh thứ hai của góc đó, đặt các đoạn thẳng OC =8 cm,OD = 10 cm
a) chứng minh hai tam giác OCB và OAD đồng dạng
b) gọi giao điểm của các cạnh AD và BC tại I, chứng minh rằng hai tam giác IAB và IDC có các góc bằng nhau từng đôi một


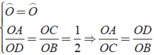


a, Ta có :
\(\frac{OA}{OC}=\frac{5}{8};\frac{OB}{OD}=\frac{10}{16}=\frac{5}{8}\)
\(\Rightarrow\frac{OA}{OC}=\frac{OB}{OD}\)
Mà góc O chung nên \(\Delta OCB~\Delta OAD\)( trường hợp 2 )
b, \(\Delta ICD , \Delta IAB\)có :
\(\widehat{CID}=\widehat{AIB}\)( đối đỉnh )
\(\widehat{CDI}=\widehat{IBA} \left(do \Delta OCB~\Delta OAD\right)\)
\(\Rightarrow\widehat{DCI}=\widehat{BAI}\)( tổng 3 góc trong tam giác )
Vậy : Hai tam giác IAB và ICD có các góc = nhau từng đôi 1