Giá trị rút gọn của
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{8-2x}{x^2+x-20}=-\dfrac{2\left(4-x\right)}{\left(4-x\right)\left(x+5\right)}=\dfrac{-2}{x+5}\)
Để biểu thức trên nhận giá trị dương khi
\(x+5< 0\)do -2 < 0
\(\Leftrightarrow x< -5\)

\(\left(\dfrac{\dfrac{x}{x+1}}{\dfrac{x^2}{x^2+x+1}}-\dfrac{2x+1}{x^2+x}\right)\dfrac{x^2-1}{x-1}\)ĐK : \(x\ne\pm1\)
\(=\left(\dfrac{x}{x+1}.\dfrac{x^2+x+1}{x^2}-\dfrac{2x+1}{x\left(x+1\right)}\right)\left(x+1\right)=\left(\dfrac{x^2+x-1}{x^2+x}-\dfrac{2x+1}{x\left(x+1\right)}\right)\left(x+1\right)\)
\(=\left(\dfrac{x^2+x-1-2x-1}{x\left(x+1\right)}\right)\left(x+1\right)=\dfrac{x^2-3x-2}{x}\)
à xin lỗi mình nhầm dòng cuối
\(=\dfrac{x^2-x-2}{x}=\dfrac{\left(x+1\right)\left(x-2\right)}{x}\)
Để biểu thức trên nhận giá trị dương khi
\(\dfrac{\left(x+1\right)\left(x-2\right)}{x}>0\)bạn tự xét TH cả tử và mẫu nhé, mình đánh trên này bị lỗi

a) a ≠ 0 , a ≠ − 5
b) Ta có A = a 3 + 4 a 2 − 5 a 2 a ( a + 5 ) = a ( a − 1 ) ( a + 5 ) 2 a ( a + 5 ) = a − 1 2
c) Thay a = -1 (TMĐK) vào a ta được A = -1
d) Ta có A = 0 Û a = 1 (TMĐK)

\(A=\dfrac{4x+8-3x+6}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x^2}{x+14}\)
\(=\dfrac{x+14}{x+14}\cdot\dfrac{x^2}{x^2-4}=\dfrac{x^2}{x^2-4}\)
Khi x=-3 thì \(A=\dfrac{\left(-3\right)^2}{\left(-3\right)^2-4}=\dfrac{9}{5}\)

\(P=\dfrac{x^2-1}{x+5}\cdot\dfrac{2x+10}{x^2-x}\) (ĐK: \(x\ne-1,x\ne0,x\ne1\))
\(P=\dfrac{\left(x-1\right)\left(x+1\right)}{x+5}\cdot\dfrac{2\left(x+5\right)}{x\left(x-1\right)}\)
\(P=\dfrac{2\left(x-1\right)\left(x+1\right)\left(x+5\right)}{x\left(x+5\right)\left(x-1\right)}\)
\(P=\dfrac{2\left(x+1\right)}{x}\)
Thay \(x=99\left(tm\right)\) vào P ta có:
\(P=\dfrac{2\left(99+1\right)}{99}=\dfrac{2\cdot100}{99}=\dfrac{200}{99}\)
\(P=\dfrac{x^2-1}{x+5}\cdot\dfrac{2x+10}{x^2-x}\\ =\dfrac{\left(x^2-1\right)\left(2x+10\right)}{\left(x+5\right)\left(x^2-x\right)}\\ =\dfrac{\left(x+1\right)\left(x-1\right)\left(x+5\right)2}{\left(x+5\right)\left(x-1\right)x}\\ =\dfrac{2x+2}{x}\)
Thay \(x=99\) vào P ta có
\(P=\dfrac{2.99+2}{99}\\ =\dfrac{200}{99}\)
Vậy \(x=99\) thì \(P=\)\(\dfrac{200}{99}\)

Bài 1:
a) Ta có: \(P=1+\dfrac{3}{x^2+5x+6}:\left(\dfrac{8x^2}{4x^3-8x^2}-\dfrac{3x}{3x^2-12}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{8x^2}{4x^2\left(x-2\right)}-\dfrac{3x}{3\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{4}{x-2}-\dfrac{x}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\dfrac{4\left(x+2\right)-x-\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}\cdot\dfrac{\left(x-2\right)\left(x+2\right)}{4x+8-x-x+2}\)
\(=1+3\cdot\dfrac{\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=1+\dfrac{3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{\left(x+3\right)\left(2x+10\right)+3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+10x+6x+30+3x-6}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+19x-6}{\left(x+3\right)\left(2x+10\right)}\)
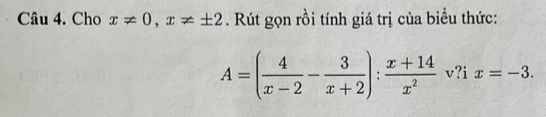
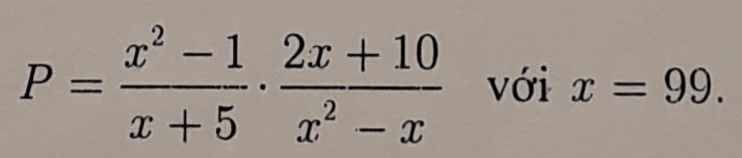
 Với
Với