Giải các hệ phương trình sau và minh họa bằng hình học kết quả tìm được: 3 2 x - y = 1 2 3 x - 2 y = 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

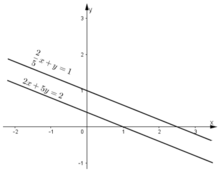
Giải các hệ phương trình sau và minh họa bằng hình học kết quả tìm được: 2 x + 5 y = 2 2 5 x + y = 1

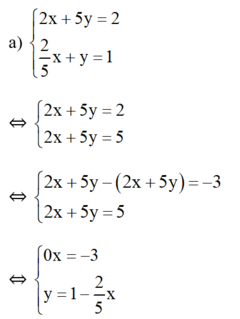
Phương trình 0x = -3 vô nghiệm nên hệ phương trình vô nghiệm.
Minh họa hình học:
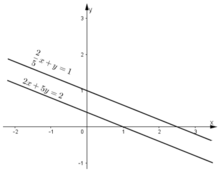
Tập nghiệm của phương trình 2x + 5y = 2 được biểu diễn bởi đường thẳng 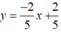 (d1)
(d1)
Tập nghiệm của phương trình 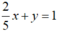 được biểu diễn bởi đường thẳng
được biểu diễn bởi đường thẳng 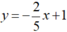 (d2).
(d2).


KL: Đồ thị hai hàm số trên song song. Điều này chứng tỏ hệ phương trình trên vô nghiệm

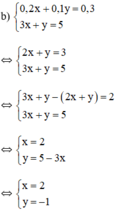
Vậy hệ phương trình có nghiệm duy nhất (2; -1).

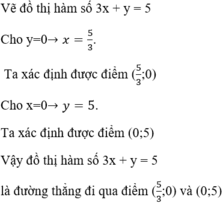
KL: Đồ thị hai hàm số trên cắt nhau tại điểm (2; -1). Vậy (2; -1) là nghiệm của hệ phương trình

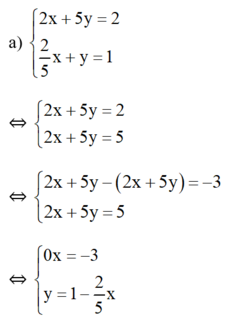
Phương trình 0x = -3 vô nghiệm nên hệ phương trình vô nghiệm.
Minh họa hình học:
Tập nghiệm của phương trình 2x + 5y = 2 được biểu diễn bởi đường thẳng 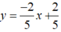 (d1)
(d1)
Tập nghiệm của phương trình 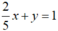 được biểu diễn bởi đường thẳng
được biểu diễn bởi đường thẳng 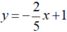 (d2).
(d2).


KL: Đồ thị hai hàm số trên song song. Điều này chứng tỏ hệ phương trình trên vô nghiệm
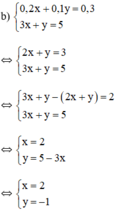
Vậy hệ phương trình có nghiệm duy nhất (2; -1).

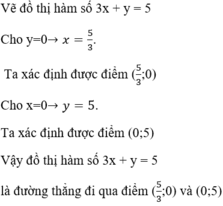
KL: Đồ thị hai hàm số trên cắt nhau tại điểm (2; -1). Vậy (2; -1) là nghiệm của hệ phương trình
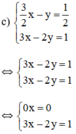
Phương trình 0x = 0 nghiệm đúng với mọi x nên hệ phương trình có vô số nghiệm dạng 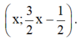


KL: Đồ thị hai hàm số trên trùng nhau. Vậy hệ phương trình có vô số nghiệm

a) Ta có: \(\left\{{}\begin{matrix}3x+y=3\\2x-y=7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5x=10\\2x-y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2x-7=2\cdot2-7=-3\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là (x,y)=(2;-3)
b) Ta có: \(7x^2-2x+3=0\)
a=7; b=-2; c=3
\(\Delta=\left(-2\right)^2-4\cdot7\cdot3=4-84=-80< 0\)
Suy ra: Phương trình vô nghiệm
Vậy: \(S=\varnothing\)

a) Giải hệ phương trình:
{2x+5y=2(1)25x+y=1(2)⇔{2x+5y=2(1′)−2x−5y=−5(2′){2x+5y=2(1)25x+y=1(2)⇔{2x+5y=2(1′)−2x−5y=−5(2′)
Cộng (1’) với (2’) vế theo vế, ta được: 0x + 0y = -3
Phương trình này vô nghiệm. Vậy hệ đã cho vô nghiệm.
Minh họa hình học kết quả tìm được:
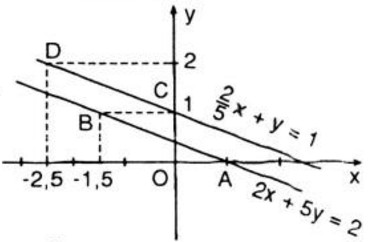
- Vẽ đồ thị hàm số 2x + 5y = 2.
Cho y = 0 ⇒ x = 1. Ta xác định được điểm A(1; 0)
Cho y = 1 ⇒ x = -1,5. Ta xác định được điểm B(-1,5; 1).
Đồ thị hàm số là đường thẳng đi qua hai điểm A và B
-Vẽ đồ thị hàm số 25x+y=1⇔2x+5y=525x+y=1⇔2x+5y=5
Cho x = 0 ⇒ y = 1. Ta xác định được điểm C(0; 1)
Cho y = 2 ⇒ x = -2,5. Ta xác định được điểm D(-2,5; 2)
Đồ thị hàm số là đường thẳng đi qua hai điểm C và D.
Kết luận: Đồ thị hai hàm số trên song song. Điều này chứng tỏ rằng hệ phương trình vô nghiệm.
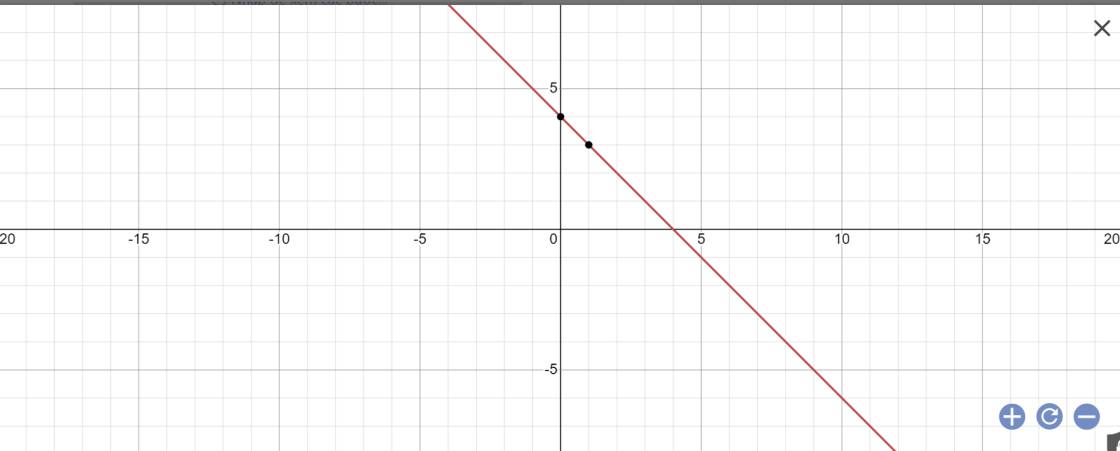
b) Giải hệ phương trình:
{0,2x+0,1y=0,3(1)3x+y=5(2)⇔{−2x−y=−3(1′)3x+y=5(2′){0,2x+0,1y=0,3(1)3x+y=5(2)⇔{−2x−y=−3(1′)3x+y=5(2′)
Cộng (1’) với (2’) vế theo vế, ta được x = 2
Thế x = 2 vào (2), ta được: 6 + y = 5 ⇔ y = -1
Vậy nghiệm của hệ phương trình là (x = 2; y = -1)
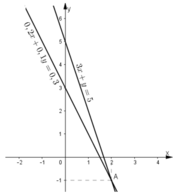
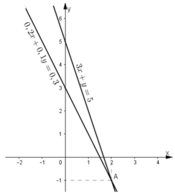
Minh họa hình học:
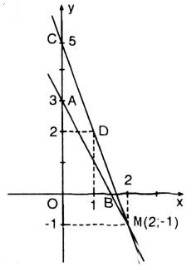
- Đồ thị hàm số 0,2x + 0,1y = 0,3 là một đường thẳng đi qua hai điểm:
A(x = 0; y = 3) và B(x = 1,5; y = 0)
- Đồ thị hàm số 3x + y = 5 là một đường thẳng đi qua hai điểm C(x = 0; y = 5) và D(x = 1; y = 2)
- Đồ thị hai hàm số trên cắt nhau tại điểm: M(x = 2; y = -1).
Vậy (2; -1) là một nghiệm của hệ phương trình.
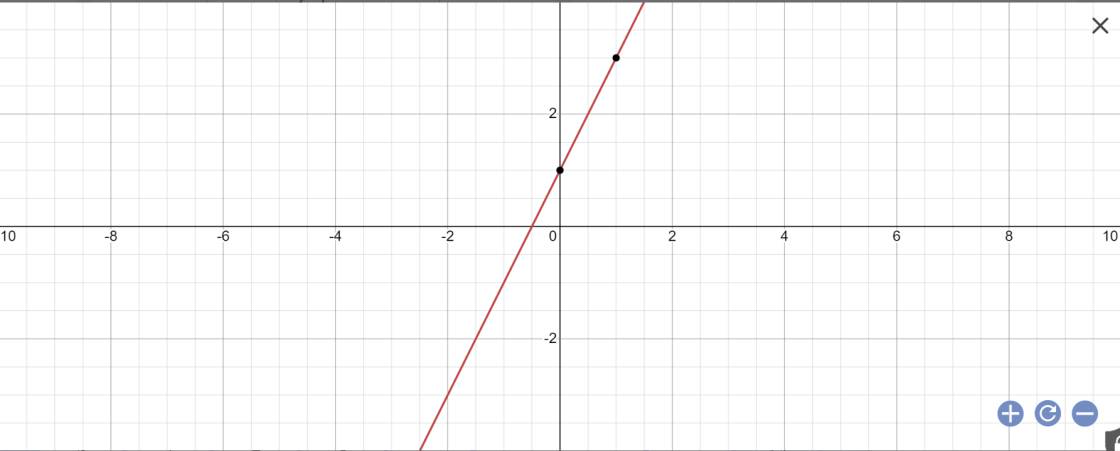
c) Giải hệ phương trình:
{32x−y=12(1)3x−2y=1(2)⇔{−3x+2y=−1(1′)3x−2y=1(2′){32x−y=12(1)3x−2y=1(2)⇔{−3x+2y=−1(1′)3x−2y=1(2′)
Cộng (1’) và (2’) vế theo vế, ta có: 0x + 0y = 0.
Phương trình này có vô số nghiệm.
Nghiệm tổng quát là (x;32x−12)(x;32x−12) với x ∈ R
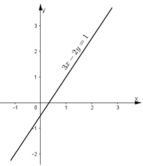
Minh họa hình học
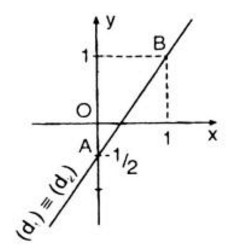
- Đồ thị hàm số (1) là đường thẳng đi qua hai điểm A(0; −12−12) và B(1;1) nên hai đường thẳng này trùng nhau. Vậy hệ phương trinh có vô số nghiệm.

Bài toán này có hai cách giải:
Cách 1: Thu gọn từng phương trình ta sẽ thu được phương trình bậc nhất hai ẩn x và y.
Cách 2: Đặt ẩn phụ.
Cách 1:
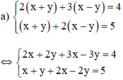
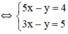 (hệ số của y bằng nhau nên ta trừ từng vế hai phương trình)
(hệ số của y bằng nhau nên ta trừ từng vế hai phương trình)
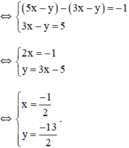
Vậy hệ phương trình có nghiệm duy nhất 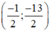
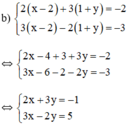
(Nhân hai vế pt 1 với 2; pt 2 với 3 để hệ số của y đối nhau)
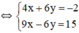 (Hệ số của y đối nhau nên ta cộng từng vế của hai pt)
(Hệ số của y đối nhau nên ta cộng từng vế của hai pt)
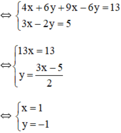
Vậy hệ phương trình có nghiệm duy nhất (1; -1).
Cách 2:
a) Đặt x + y = u và x – y = v (*)
Khi đó hệ phương trình trở thành
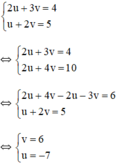
Thay u = -7 và v = 6 vào (*) ta được hệ phương trình:
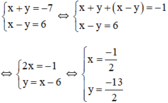
Vậy hệ phương trình có nghiệm 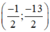
b) Đặt x – 2 = u và y + 1 = v.
Khi đó hệ phương trình trở thành :
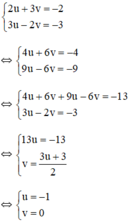
+ u = -1 ⇒ x – 2 = -1 ⇒ x = 1.
+ v = 0 ⇒ y + 1 = 0 ⇒ y = -1.
Vậy hệ phương trình có nghiệm (1; -1).
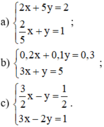
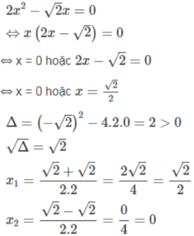
Phương trình 0x = 0 nghiệm đúng với mọi x nên hệ phương trình có vô số nghiệm dạng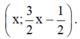
KL: Đồ thị hai hàm số trên trùng nhau. Vậy hệ phương trình có vô số nghiệm