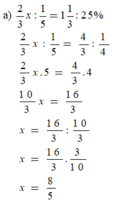
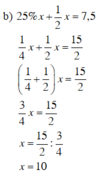
a/ \(x-\dfrac{3}{7}=\dfrac{2}{5}\cdot\dfrac{1}{4}\)

\(x-\dfrac{3}{7}=\dfrac{1}{10}\)

\(x=\dfrac{1}{10}+\dfrac{3}{7}=\dfrac{37}{70}\)

Vậy....

b/ \(x+\dfrac{4}{5}=-\dfrac{5}{12}\cdot\dfrac{3}{25}\)

\(x+\dfrac{4}{5}=-\dfrac{1}{20}\)

\(x=-\dfrac{1}{20}-\dfrac{4}{5}=-\dfrac{17}{20}\)

Vậy....

c/ \(\dfrac{x}{182}=-\dfrac{6}{12}\cdot\dfrac{35}{91}\)

\(\dfrac{x}{182}=-\dfrac{5}{26}\)

\(=>x\cdot26=-5\cdot182\)

\(26x=-910\)

\(x=-910:26=-35\)

Vậy....

a) Ta có: \(x-\dfrac{3}{7}=\dfrac{2}{5}\cdot\dfrac{1}{4}\)

\(\Leftrightarrow x-\dfrac{3}{7}=\dfrac{1}{10}\)

\(\Leftrightarrow x=\dfrac{1}{10}+\dfrac{3}{7}=\dfrac{7}{70}+\dfrac{30}{70}\)

hay \(x=\dfrac{37}{70}\)

Vậy: \(x=\dfrac{37}{70}\)

a) Ta có: \(\dfrac{x}{3}=\dfrac{7}{25}+\dfrac{-1}{5}\)

\(\Leftrightarrow\dfrac{x}{3}=\dfrac{7}{25}+\dfrac{-5}{25}=\dfrac{2}{25}\)

hay \(x=\dfrac{6}{25}\)

Vậy: \(x=\dfrac{6}{25}\)

b) Ta có: \(\dfrac{4}{9}+\dfrac{x}{5}=\dfrac{5}{11}\)

\(\Leftrightarrow\dfrac{x}{5}=\dfrac{5}{11}-\dfrac{4}{9}=\dfrac{45}{99}-\dfrac{44}{99}=\dfrac{1}{99}\)

hay \(x=\dfrac{5}{99}\)

Vậy: \(x=\dfrac{5}{99}\)

Bài 1: 

a) Ta có: \(\dfrac{17}{6}-x\left(x-\dfrac{7}{6}\right)=\dfrac{7}{4}\)

\(\Leftrightarrow\dfrac{17}{6}-x^2+\dfrac{7}{6}x-\dfrac{7}{4}=0\)

\(\Leftrightarrow-x^2+\dfrac{7}{6}x+\dfrac{13}{12}=0\)

\(\Leftrightarrow-12x^2+14x+13=0\)

\(\Delta=14^2-4\cdot\left(-12\right)\cdot13=196+624=820\)

Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:

\(\left\{{}\begin{matrix}x_1=\dfrac{14-2\sqrt{205}}{-24}=\dfrac{-7+\sqrt{205}}{12}\\x_2=\dfrac{14+2\sqrt{2015}}{-24}=\dfrac{-7-\sqrt{205}}{12}\end{matrix}\right.\)

b) Ta có: \(\dfrac{3}{35}-\left(\dfrac{3}{5}-x\right)=\dfrac{2}{7}\)

\(\Leftrightarrow\dfrac{3}{5}-x=\dfrac{3}{35}-\dfrac{10}{35}=\dfrac{-7}{35}=\dfrac{-1}{5}\)

hay \(x=\dfrac{3}{5}-\dfrac{-1}{5}=\dfrac{3}{5}+\dfrac{1}{5}=\dfrac{4}{5}\)

ai giúp mik vs

a \(\dfrac{2}{3}x+\dfrac{1}{3}=\dfrac{1}{5}\\ \dfrac{2}{3}x=\dfrac{1}{5}-\dfrac{1}{3}\\ \dfrac{2}{3}x=\dfrac{-2}{15}\\ x=-\dfrac{2}{15}:\dfrac{2}{3}\\ x=-\dfrac{1}{5}\)   b) \(\dfrac{4}{5}-\dfrac{5}{3}x=-2\\ \dfrac{5}{3}x=\dfrac{4}{5}+2\\ \dfrac{5}{3}x=\dfrac{14}{5}\\ x=\dfrac{14}{5}:\dfrac{5}{3}\\ x=\dfrac{42}{25}\)c) \(\dfrac{1}{5}+\dfrac{5}{3}:x=\dfrac{1}{2}\\ \dfrac{5}{3}:x=\dfrac{1}{2}-\dfrac{1}{5}\\ \dfrac{5}{3}:x=\dfrac{3}{10}\\ x=\dfrac{5}{3}:\dfrac{3}{10}\\ x=\dfrac{50}{9}\)d) \(\dfrac{5}{7}:x-3=-\dfrac{2}{7}\\ \dfrac{5}{7}:x=3-\dfrac{2}{7}\\ \dfrac{5}{7}:x=\dfrac{19}{7}\\ x=\dfrac{5}{7}:\dfrac{19}{7}\\ x=\dfrac{5}{19}\)

Mơn

\(B1\\ a,2x+10y=2\left(x+5y\right)\\ b,x^2+4x+4=x^2+2.2x+2^2=\left(x+2\right)^2\\ c,x^2-y^2+10y-25\\ =\left(x^2-y^2\right)+5\left(2y-5\right)\\ =\left(x-y\right)\left(x+y\right)+5\left(2y-5\right)\\ B2\)

\(a,x^2-3x+x-3=0\\ =>x\left(x-3\right)+\left(x-3\right)=0\\ =>\left(x+1\right)\left(x-3\right)=0\\ =>\left[{}\begin{matrix}x+1=0\\x-3=0\end{matrix}\right.=>\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\\ b,2x\left(x-3\right)-\dfrac{1}{2}\left(4x^2-3\right)=0\\ =>2x^2-6x-2x^2+\dfrac{3}{2}=0\\ =>-6x=-\dfrac{3}{2}\\ =>x=\left(-\dfrac{3}{2}\right):\left(-6\right)\\ =>x=\dfrac{1}{4}\\ c,x^2-\left(x-3\right)\left(2x-5\right)=9\\ =>x^2-2x^2+6x+5x-15=9\\ =>-x^2+11-15-9=0\\ =>-x^2+11x-24=0\\ =>-x^2+8x+3x-24=0\\ =>-x\left(x-8\right)+3\left(x-8\right)=0\\ =>\left(3-x\right)\left(x-8\right)=0\\ =>\left[{}\begin{matrix}3-x=0\\x-8=0\end{matrix}\right.=>\left[{}\begin{matrix}x=3\\x=8\end{matrix}\right.\)

`#3107.101107`

`1.`

`a,`

`(2x - 3)^2 = |3 - 2x|`

`=> (2x - 3)^2 = |2x - 3|`

`=>`\(\left[{}\begin{matrix}2x-3=\left(2x-3\right)^2\\2x-3=-\left(2x-3\right)^2\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}2x-3-\left(2x-3\right)^2=0\\2x-3+\left(2x-3\right)^2=0\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}\left(2x-3\right)\left(1-2x+3\right)=0\\\left(2x-3\right)\left(1+2x-3\right)=0\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}2x-3=0\\4-2x=0\\2x-2=0\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=2\\x=1\end{matrix}\right.\)

Vậy, `x \in {3/2; 2; 1}`

`b,`

`(x - 1)^2 + (2x - 1)^2 = 0`

`=>`\(\left[{}\begin{matrix}\left(x-1\right)^2=0\\\left(2x-1\right)^2=0\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}x-1=0\\2x-1=0\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}x=1\\x=\dfrac{1}{2}\end{matrix}\right.\)

Vậy, `x \in {1; 1/2}`

`c,`

`5 - x^2 = 1`

`=> x^2 = 4`

`=> x^2 = (+-2)^2`

`=> x = +-2`

Vậy, `x \in {-2; 2}`

`d,`

`x - 2\sqrt{x} = 0`

`=> x^2 - (2\sqrt{x})^2 = 0`

`=> x^2 - 4x = 0`

`=> x(x - 4) = 0`

`=>`\(\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)

Vậy, `x \in {0; 4}`

`g,`

`(x - 1) + 1/7 = 0`

`=> x - 1 + 1/7 = 0`

`=> x - 6/7 = 0`

`=> x = 6/7`

Vậy, `x = 6/7.`

giúp mình giải bài toán trên với. Mình cảm ơn rất nhiều

a: =>1/2x-3/4x=-5/6+7/3

=>-1/4x=14/6-5/6=3/2

=>x=-3/2*4=-6

b: =>4/5x-3/2x=1/2+6/5

=>-7/10x=17/10

=>x=-17/7

c: =>6/5x+6/20=6/5-1/3x

=>6/5x+1/3x=6/5-3/10=12/10-3/10=9/10

=>x=27/46

d: =>6x+3/2+4/5=1/2-2x

=>8x=1/2-3/2-4/5=-1-4/5=-9/5

=>x=-9/40

2:

a: x=2,4-0,4=2

b: =>2x=-1,5+0,8=-0,7

=>x=-0,35

c: =>x-16=-15

=>x=1

Lời giải:
a.

$0< x< \frac{1}{4}+\frac{4}{5}$

$\Rightarrow 0< x< \frac{21}{20}$ hay $0< x< 1,05$

$\Rightarrow x=1$

b.

$\frac{4}{7}+\frac{3}{7}< x< \frac{5}{3}+\frac{2}{3}$
$\Rightarrow 1< x< \frac{7}{3}$
$\Rightarrow x=2$

cha loi di