Từ độ cao 63m của tháp nghiêng PISA ở Italia (H.5) người ta thả một quả bóng cao su xuống đất. Giả sử mỗi lần chạm đất quả bóng lại nảy lên một độ cao bằng 1/10 độ cao mà quả bóng đạt được ngay trướcđó.
Tính độ dài hành trình của quả bóng từ thờiđiểm ban đầu cho đến khi nó nằm yên trên mặt đất.




Mỗi khi chạm đất quả bóng lại nảy lên một độ cao bằng 1/10 độ cao của lần rơi ngay trước đó và sau đó lại rơi xuống từ độ cao thứ hai này. Do đó, độ dài hành trình của quả bóng kể từ thời điểm rơi ban đầu đến:
- Thời điểm chạm đất lần thứ nhất là d 1 = 63
- Thời điểm chạm đất lần thứ hai là:
- Thời điểm chạm đất lần thứ ba là:
- Thời điểm chạm đất lần thứ tư là:
....
- Thời điểm chạm đất lần thứ n (n > 1) là
(Có thể chứng minh khẳng định này bằng quy nạp).
Do đó, độ dài hành trình của quả bóng kể từ thời điểm rơi ban đầu đến khi nằm yên trên mặt đất là :
Vì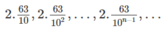
là một cấp số nhân lùi vô hạn, công bội q = 1/10 nên ta có
Vậy