Không gian mẫu:  n Ω = 6 . 6 = 36

Gọi A là biến cố: ‘‘Tổng số chấm xuất hiện hai lần tung là một số nhỏ hơn 10’’.

⇒ A ¯ : ‘‘Tổng số chấm xuất hiện hai lần tung là một số không nhỏ hơn 10’’.

Tổng số chấm là một số không nhỏ hơn 10 nên số chấm xuất hiện là các cặp: 

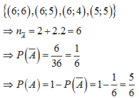
Chọn B.

Rõ ràng \(\Omega=\left\{\left(i;j\right):1\le i,j\le6\right\}\)

Kí hiệu :

\(A_1:\) "Lần đầu xuất hiện mặt 1 chấm"

\(B_1:\) "Lần thứ hai xuất hiện mặt 1 chấm"

\(C:\) " Tổng số chấm là 6"

\(D:\) "Mặt 1 chấm xuất hiện ít nhất một lần"

a) Ta có \(C=\left\{\left(1,5\right),\left(5,1\right),\left(2,4\right),\left(4,2\right)\left(3,3\right)\right\},P\left(C\right)=\dfrac{5}{36}\)

b) Ta có \(A_1,B_1\) độc lập và \(D=A_1\cup B_1\) nên

\(P\left(D\right)=P\left(A_1\right)+P\left(B_1\right)-P\left(A_1B_1\right)\)

\(=\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{6}.\dfrac{1}{6}=\dfrac{11}{36}\)

Chọn D

Ta có số phần tử của không gian mẫu là  n ( Ω ) = 36

Phương trình  1 2 x 2   +   6 x   +   m   =   0  có hai nghiệm phân biệt khi và chỉ khi

Khi đó số chấm trên hai con con súc sắc là cặp số (i;j) với i,j =  1 , 6 ¯  thỏa mãn

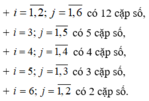
Như thế, có tất cả 12 + 5 + 4 + 3 +2 = 26 cặp số (i;j) để i.j = m < 18

Vậy xác suất cần tìm bằng  26 36

Xác suất:

a. \(\dfrac{3}{6}.\dfrac{3}{6}=\dfrac{1}{4}\)

b. \(\dfrac{6}{36}=\dfrac{1}{6}\)

c. Xác suất mặt 6 chấm ko xuất hiện lần nào: \(\dfrac{5}{6}.\dfrac{5}{6}=\dfrac{25}{36}\)

Xác suất mặt 6 xuất hiện ít nhất 1 lần: \(1-\dfrac{25}{36}=\dfrac{11}{36}\)

d. Các trường hợp tổng 2 mặt lớn hơn hoặc bằng 10: (6;4), (4;6); (5;5); (5;6);(6;5);(6;6) có 6 khả năng

\(\Rightarrow36-6=30\) khả năng tổng số chấm bé hơn 10

Xác suất: \(\dfrac{30}{36}=\dfrac{5}{6}\)

Số phần tử của không gian mẫu là: `n(Ω)=6`

A: "Số chấm xuất hiện nhỏ hơn ba"

`-> n(A)= 2`

`=> P(A)=(n(Ω))/(n(A))=2/6=1/3`

`=>` A. 

Chọn A

A

A

Gọi B là biến cố: “Tổng số chấm xuất hiện trên bề mặt con súc sắc bằng 12”

Ta thấy

12 = 1 + 5 + 6 = 2 + 4 + 6 = 2 + 5 + 5 = 3 + 3 + 6 = 3 + 4 + 5 = 4 + 4 + 4

Nếu số chấm trên bề mặt 3 con súc sắc khác nhau tức là các trường hợp (1;5;6), (2;4;6), (3;4;5) có 3 ! .3 = 18  cách

Nếu số chấm trên bề mặt 3 con súc sắc có 2 con giống nhau tức là các trường hợp (2;5;5) và (3;3;6) có 3.2 = 6  cách

Nếu số chấm trên bề mặt 3 con súc sắc giống nhau ta có 1 cách gieo duy nhất

⇒ n B = 18 + 6 + 1 = 25 . Vậy P B = n B Ω B = 25 216 .

Chọn A

Chọn C

Không gian mẫu: “ gieo ngẫu nhiên một con súc sắc 3 lần liên tiếp” 

Biến cố A: “ số  a b c ¯  chia hết cho 45”

a b c ¯  chia hết cho 45  ⇔ a b c ¯ chia hết cho cả 5 và 9

Vì  a b c ¯ chia hết cho 5 nên là số chấm xuất hiện của súc sắc khi gieo).

Vì  a b c ¯  chia hết cho 9 mà c = 5 => a + b + 5 chia hết cho 9.

Các cặp số (a;b) sao cho  mà a+b+5 chia hết cho 9 là: (1;3), (3;1), (2;2)

Do đó: n(A) = 3.