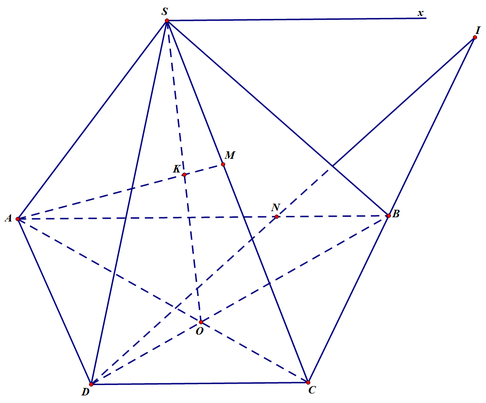
Cho hình Chóp S.ABCD có đáy là hình thang, đáy lớn AB. Gọi O là giao điểm của AC và BD
a. Tìm giao tuyến của hai mặt phẳng (SAD) và (SAB), (SAB)và (SCD)
b. Trên SC lấy điểm M tùy ý. Tìm giao điểm K của SD và mp (ABM)
c. Tìm thiết diện của hình chóp với mặt phẳng (ABM)
giúp mình với