Cho hình lập phương ABCD. A’B’C’D’. Hình chiếu vuông góc của A lên mặt phẳng (A’BD) là:
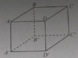
A. trung điểm của BD
B. trung điểm của A’B
C. trung điểm của A’D
D. tâm O của tam giác BDA’
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
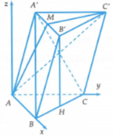
Gọi H là trung điểm của cạnh BC. Suy ra B ' H ⊥ A B C
∆ A B C vuông tại A nên B C = A B 2 + A C 2 = 5
vuông tại H nên B ' H = B ' B 2 - B H 2 = 3
Chọn hệ trục tọa độ Oxyz như hình, trong đó A ≡ O 0 ; 0 ; 0 , B 3 ; 0 ; 0 , C 0 ; 4 ; 0 .
Ta có H là trung điểm của BC nên H 3 2 ; 2 ; 0 , H là hình chiếu của B’ trên bề mặt phẳng (ABC) nên B ' 3 2 ; 2 ; 3 .
Từ A B ⇀ = A ' B ' ⇀ suy ra
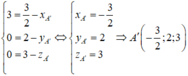
Từ A C ⇀ = A ' C ' ⇀ suy ra
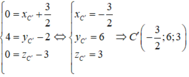
M là trung điểm của A’B’ nên M(0;2;3).
Ta có
![]()
![]()
Mặt phẳng (AMC’) có một vectơ pháp tuyến là n 1 ⇀ = 8 ; 3 ; - 2 .
Lại có A ' B ⇀ = 9 2 ; - 2 ; - 3 , A ' C ⇀ = 3 2 ; 2 ; - 3
⇒ A ' B ⇀ , A ' C ⇀ = 12 ; 9 ; 12
⇒ Mặt phẳng (A’BC) có một vectơ pháp tuyến là n 2 ⇀ = 4 ; 3 ; 4 .
Gọi α là góc tạo bởi hai mặt phẳng (AMC’) và (A’BC) thì:
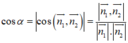
⇒ cos α = 33 3157
Gọi M là trung điểm của BD, là trung điểm của A’B.
Suy ra tâm O của tam giác BDA’ là giao của DN và A’M
Phương án D đúng vì BD ⊥ (AMA') bởi BD ⊥ AM và BD ⊥ A’M ⇒ BD ⊥ AO
BA’ ⊥ (AND) do BA’ ⊥ DN và A’B ⊥ AN ⇒ A’B ⊥ AO
AO ⊥ (A’BD) ⇒ O là hình chiếu của A trên (A’BD).
Đáp án D