Chọn D.

Gọi cấp số nhân đó là (u_n), n = 1,7 ¯ . Theo đề bài ta có :

u 4 = 6 u 7 = 243 u 2 ⇔ u 1 . q 3 = 6 u 1 . q 6 = 243 u 1 . q ⇔ u 1 = 2 9 q = 3

Do đó các số hạng còn lại của cấp số nhân là

u 1 = 2 9 ; u 2 = 2 3 ; u 3 = 2 ; u 5 = 18 ; u 6 = 54 ; u 7 = 162

Đáp án A

+ Gọi số hạng đầu của cấp số nhân là u1, công bội là x

Theo giả thiết ta có hệ phương trình

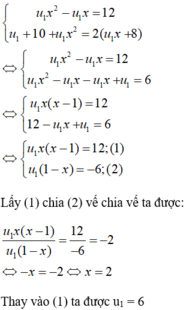
+ Tổng của năm số hạng đầu của CSN là:

Gọi 3 số hạng của cấp số cộng là: \(5;5+d;5+2d\)
Gọi 3 số hạng của cấp số nhân là: \(5;5q;5q^2\).
Ta có hệ sau:\(\left\{{}\begin{matrix}5+2d=5q^2\\5+d=5q+10\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}5+2d=5q^2\\d=5q+5\end{matrix}\right.\)\(\Rightarrow5+2.\left(5q+5\right)=5q^2\)\(\Rightarrow\left\{{}\begin{matrix}q=-1\\q=3\end{matrix}\right.\).
Với \(q=-1\) thì \(d=5.q+5=5.\left(-1\right)+5=0\).
Với \(q=3\) thì \(d=5.q+5=5.3+5=20\).
Vậy
Với \(q=-1\):
3 số hạng của cấp số cộng là: 5; 5; 5.
3 số hạng của cấp số nhân là: 5; - 5; 5.
Với \(q=3\):
3 số hạng của cấp số cộng là: 5; 25; 45.
3 số hạng của cấp số nhân là: 5; 15; 45.

Số hạng tổng quát của cấp số cộng: \({u_n} = {u_1} \times {q^{n - 1}}\).

Ta có: \(\left\{ \begin{array}{l}{u_6} = {u_1}{q^5} = 96\\{u_3} = {u_1}{q^2} = 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1}{q^2}.{q^3} = 96\\{u_1}{q^2} = 12\end{array} \right.\).

\( \Leftrightarrow \left\{ \begin{array}{l}12.{q^3} = 96\\{u_1}{q^2} = 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}q = 2\\{u_1} = 3\end{array} \right.\)

\( \Rightarrow {u_n} = 3 \times {2^{n - 1}}\).

Số hạng thứ 50: \({u_{50}} = 3 \times {2^{50 - 1}} = 3 \times {2^{49}}\).

Chọn đáp án D

u 4 = u 1 . q 3 = 48

Chọn đáp án D

ĐS: Cấp số cộng: 5, 25, 45

Cấp số nhân: 5, 15, 45

Kí hiệu u1,u2,u3,u4,u5 là các số hạng của cấp số nhân

Ta có :

Đáp án C