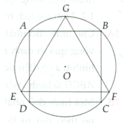
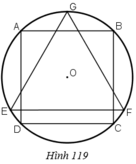
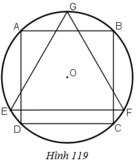
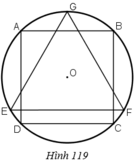
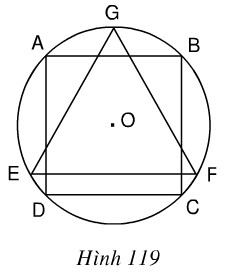
Cho hình vuông ABCD nội tiếp đưòng tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đuờng tròn đó, EF là dây song song với AB. Cho hình đó quay xung quanh trục GO. Chứng minh:
a, Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra
b, Bình phương diện tích toàn phần của hình trụ bằng tích diện tích hình cầu và diện tích toàn phần của hình nón


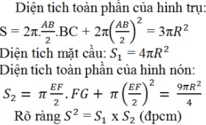

-0132.jpg)
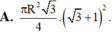
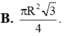
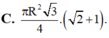
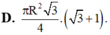

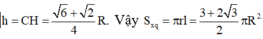
a, V h t A B C D = π AB 2 2 . BC = π AB 3 4 = π 2 2 . R 3 (1)
V h c = 4 3 πR 3 (2)
V h n = 1 3 π EF 2 2 . GH = 1 8 3 π . EF 3 . Tính được GO = 3 R
=> V h n = 1 8 3 π 3 3 R 3 = 3 8 πR 3 (3)
Từ (1), (2) và (3) => ĐPCM
b, S t p h t = 3 πR 2 (4); S h c = 4 πR 2 (5)
S t p h n = 3 4 πEF 2 = 3 4 π . 3 R 2 = 9 4 πR 2 (6)
Từ (4); (5) và (6) => ĐPCM