Xét tam giác NMB và tam giác NMC có NM là cạnh chung.

=> NB= NC

=> MB = MC ( Vì M là trung điểm của BC )

Vậy NMB = NMC ( c.c.c)

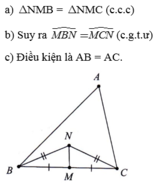
a) Xét \(\Delta\) NMB và \(\Delta\)NMC có 

\(MB=MC\left(gt\right)\)

\(MN\) là cạnh chung

\(\widehat{M_1}=\widehat{M_2}=90^o\)

\(\Delta NMB=\Delta NMC\left(c-g-c\right)\)( cạnh-góc-cạnh)

 b) \(\Rightarrow\widehat{MBN}=\widehat{MCN}\)

Có : NB = NC

=> tam giác NBC cân tại N

Có : NM vừa là đường trung tuyến vừa là đường cao

=> NM vuông góc với BC

Xét tam giác NMB và tam giác NMC có:

NM = NC

Cạnh NM chung

Góc NMB = NMC = 90⁰

=> tám giác NMB = NMC (cạnh huyền cạnh góc vuông) (đpcm)

xét tam giác NMB và tam giác NMC ta có:

NB=NC(gt)

BM=MC(gt)

MN:cạnh chung

kết hợp ba cái trên . Suy ra tam giác NMB=tam giác NMC

\(\left\{{}\begin{matrix}NB=NC\\MB=MC\\MN.chung\end{matrix}\right.\Rightarrow\Delta NMB=\Delta NMC\left(c.c.c\right)\\ \Rightarrow\widehat{NMB}=\widehat{NMC}\)

Mà \(\widehat{NMB}+\widehat{NMC}=180^0\Rightarrow\widehat{NMB}=\widehat{NMC}=90^0\)

\(\Rightarrow MN\perp BC\left(1\right)\)

\(\left\{{}\begin{matrix}AB=AC\\MB=MC\\MA.chung\end{matrix}\right.\Rightarrow\Delta AMB=\Delta AMC\left(c.c.c\right)\\ \Rightarrow\widehat{AMB}=\widehat{AMC}\)

Mà \(\widehat{AMB}+\widehat{AMC}=180^0\Rightarrow\widehat{AMB}=\widehat{AMC}=90^0\)

\(\Rightarrow AM\perp BC\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow AM\equiv MN\)

Vậy A,N,M thẳng hàng

Hình bạn tự vẽ nha :) Mình làm phần a) nhé

a) Xét \(\Delta NMB\) và \(\Delta NMC\) có :

Bm = MC ( vì M là trung điểm )

NM : cạnh chung

NB = NC ( gt )

=> \(\Delta NMB\) = \(\Delta NMC\)

Hình bạn tự vẽ đc chớ nhỉ

a) Xét \(\Delta\) MNB và \(\Delta\) MNC có

MN : cạnh chung

MB = MC  ( do M là trung điểm của BC )

NB = NC  ( gt)

=>\(\Delta\) MNB = \(\Delta\)MNC   ( c-c-c)

b) Theo câu a ta có

​​​\(\Delta\)​ MNB = \(\Delta\)MNC 

=> \(\widehat{NMB}=\widehat{NMC}\)​  ( 2 góc tương ứng )     (1) 

Mà \(\widehat{NMB}+\widehat{NMC}=180^o\)    ( 2 góc kề bù )     (2)

Từ (1) và (2) =>  ​ ​\(\widehat{NMB}=\widehat{NMC}=\frac{180^o}{2}=90^o\)  (*1)

Lại có MN cắt BC tại M    (*2)

Từ (*1) và (*2)  => \(MN\perp BC\) tại M

@@ Học tốt

Takigawa Miu_