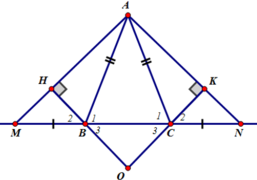
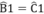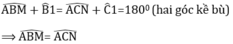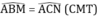Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối tia của tia CB lấy điểm N sao cho BM = CN.
a) Chứng minh tam giác AMN cân.
b) Kẻ B E ⊥ A M ( E ∈ A M ) , C F ⊥ A N ( F ∈ A N ) . Chứng minh ∆ B M E = ∆ C N F .
c) EB và FC kéo dài cắt nhau tại O. Chứng minh AO là tia phân giác của góc MAN.
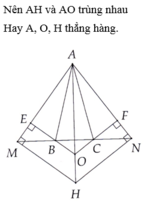
d) Qua M kẻ đường thẳng vuông góc với AM, qua N kẻ đường thẳng vuông góc với AN, chúng cắt nhau ở H. Chứng minh ba điểm A, O, H thẳng hàng.


 Bn tham khảo nhé!
Bn tham khảo nhé!