Giải và biện luận các phương trình sau theo tham số m.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Điều kiện của phương trình là x ≠ -1, ta có
![]()
⇒ (m - 2)x + 3 = (2m - 1)(x + 1)
⇒ (m + 1)x = 4 - 2m (1)
Với m = -1 phương trình (1) vô nghiệm nên phương trình đã cho cũng vô nghiệm.
Với m ≠ -1 phương tình (1) có nghiệm ![]()
Nghiệm này thỏa mãn điều kiện x ≠ -1 khi và chỉ khi 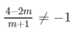 hay -2m + 4 ≠ -m - 1 ⇒ m ≠ 5
hay -2m + 4 ≠ -m - 1 ⇒ m ≠ 5
Kết luận
Với m = -1 hoặc m = 5 phương trình vô nghiệm
Với m ≠ -1 và m ≠ 5 phương trình có nghiệm là ![]()

Với m = -1 phương trình đã cho trở thành
-5x + 1 = 0 ⇔ x = 1/5
Với m ≠ -1 phương trình đã cho là một phương trình bậc hai, có biệt thức Δ = -24m + 1
Nếu m ≤ 1/24 thì Δ ≥ 0 phương trình có hai nghiệm

Với m = -1 phương trình có nghiệm là x = 1/5

Điều kiện của phương trình là x ≠ 1. Khi đó ta có
![]()
⇔ (2m + 1)x - m = (x + m)(x - 1)
⇔ x2 - (m + 2)x = 0
⇔ x = 0, x = m + 2
Giá trị x = m + 2 thỏa mãn điều kiện của phương trình khi m ≠ -1
Kết luận
Vậy với m = -1 phương trình có nghiệm duy nhất x = 0;
Với m ≠ -1 phương trình có hai nghiệm x = 0 và x = m + 2.

Điều kiện của phương trình là x ≠ m . Khi đó ta có
![]()
⇔ (3m - 2)x - 5 = -3x + 3m
⇔ (3m + 1)x = 3m + 5
Với m ≠ -1/3 nghiệm của phương trình cuối là ![]()
Nghiệm này thỏa mãn điều kiện của phương trình khi và chỉ khi
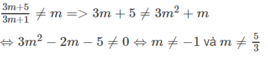
Kết luận
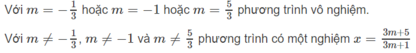

Phương trình đã cho tương đương với phương trình
( m 2 - 6 m + 8 ) x = m 2 - m - 2
⇔ (m - 2)(m - 4)x = (m + 1)(m - 2)
Kết luận
Với x ≠ 2 và x ≠ 4 phương trình có nghiệm ![]()
Với m = 2, mọi số thực x đều là nghiệm của phương trình;
Với m = 4, phương trình vô nghiệm.

Với ![]() phương trình đã cho trở thành
phương trình đã cho trở thành
3x + 2m = x - m ⇔ 2x = -3m ⇔ x = -3m / 2
Ta có:
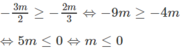
Với ![]() Phương trình đã cho trở thành
Phương trình đã cho trở thành
-3x - 2m = x - m ⇔ 4x = -m ⇔ x = -m / 4
Ta có:
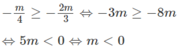
Kết luận
Với m > 0 phương trình vô nghiệm;
Với m = 0 phương trình có nghiệm x = 0;
Với m < 0 phương trình có nghiệm
![]()

Điều kiện của phương trình là m ≠ 1/2. Khi đó ta có
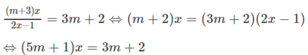
Nếu m ≠ -1/5 thì phương trình có nghiệm ![]()
Giá trị này là nghiệm của phương trình đã cho khi
![]()
Nếu m = -1/5 phương trình cuối vô nghiệm.
Kết luận.
Với m = -1/5 hoặc m = -3 phương trình đã cho vô nghiệm.
Với m ≠ -1/5 và m ≠ -3 nghiệm của phương trình đã cho là
![]()

Điều kiện của phương trình là m > 1/2
Với điều kiện đó vế trái dương, nên vế phải cũng dương nên m > 1. Lúc đó ta có:
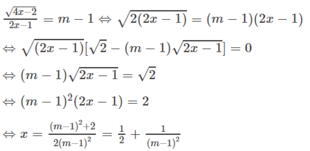
Giá trị ![]() thỏa mãn điều kiện x > 1/2
thỏa mãn điều kiện x > 1/2
Kết luận. Với m ≤ 1 phương trình vô nghiệm.
Với m > 1 nghiệm của phương trình là
![]()

![]()
Phương trình (1) ⇔ x = -3m + 2
Phương trình (2) ⇔ 3x = m - 2 ⇔ x = (m - 2) / 3
Vậy với mọi giá trị của m phương trình có nghiệm là:
x 1 = -3m + 2 và x 2 = (m - 2) / 3
Điều kiện của phương trình là: x ≠ 3. Ta có:
Kết luận
Với m ≠ 1/4 phương trình đã cho có hai nghiệm và x = 3/2 và x = (7 - 4m)/2
Với m ≠ 1/4 phương trình có một nghiệm x = 3/2