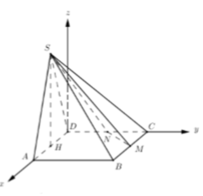
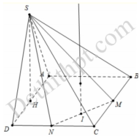
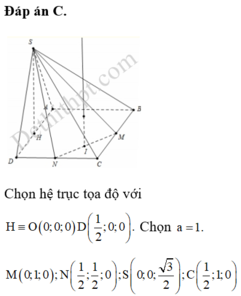
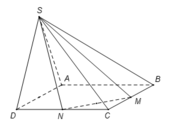
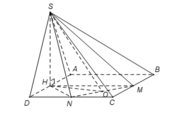
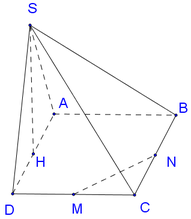
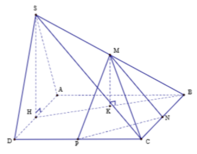
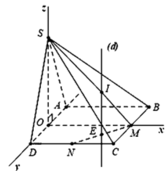
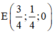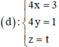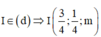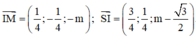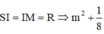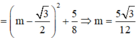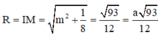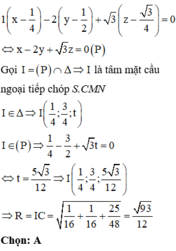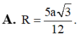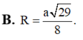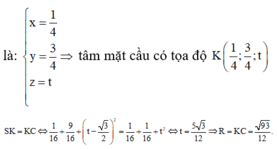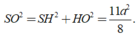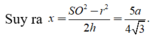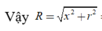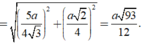Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAD đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Gọi M và N lần lượt là trung điểm của BC và CD. Tính thể tích khối chóp S.CMN.
A. V = a 3 3 18
B. V = a 3 3 24
C. V = a 3 3 48
D. V = a 3 3 8


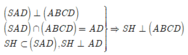
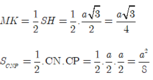
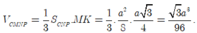
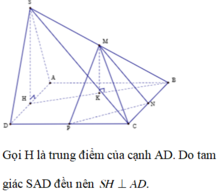

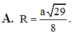
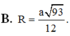

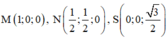 =>
=>