Cho hàm số f x = x + 4 - 2 x , x > 0 m x + m + 1 4 , x ≤ 0 , m là tham số. Tìm giá trị của tham số m để hàm số có giới hạn tại x = 0.
A. m = 1
B. m = 0
C. m = 1 2
D. m = - 1 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: \(f'\left(x\right)=\dfrac{1}{3}\cdot3x^2+2x-\left(m+1\right)=x^2+2x-m-1\)
\(\Delta=2^2-4\left(-m-1\right)=4m+8\)
Để f'(x)>=0 với mọi x thì 4m+8<=0 và 1>0
=>m<=-2
=>\(m\in\left\{-10;-9;...;-2\right\}\)
=>Có 9 số

Chọn A
Dựa vào đồ thị của hàm f'(x) ta có bảng biến thiên.
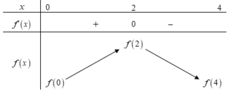
Vậy giá trị lớn nhất M = f(2)
Hàm số đồng biến trên khoảng (0;2) nên f(2) > f(1) => f(2) - f(1) > 0 .
Hàm số nghịch biến trên khoảng (2;4) nên f(2) > f(3) => f(2) - f(3) > 0.
Theo giả thuyết: f(0) + f(1) - 2f(2) = f(4) - f(3).
![]()
=> f(0) > f(4)
Vậy giá trị nhỏ nhất m = f(4)

Chọn B
Từ đồ thị của hàm số f'(x) trên đoạn [0;4] ta có bảng biến thiên của hàm số trên đoạn [0;4] như sau:
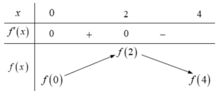
Từ bảng biến thiên ta có ![]()
Mặt khác ![]()
![]()
![]()
![]()
Suy ra ![]()

\(h\left(x\right)=f\left(x^2+1\right)-m\Rightarrow h'\left(x\right)=2x.f'\left(x^2+1\right)\)
\(h'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\f'\left(x^2+1\right)=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x^2+1=2\\x^2+1=5\end{matrix}\right.\) \(\Rightarrow x=\left\{-2;-1;0;1;2\right\}\)
Hàm có nhiều cực trị nhất khi \(h\left(x\right)=m\) có nhiều nghiệm nhất
\(f\left(x\right)=\int f\left(x\right)dx=\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x+C\)
\(f\left(1\right)=0\Rightarrow C=-\dfrac{199}{12}\Rightarrow f\left(x\right)=-\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x-\dfrac{199}{12}\)
\(x=\pm2\Rightarrow x^2+1=5\Rightarrow f\left(5\right)\approx-18,6\)
\(x=\pm1\Rightarrow x^2+1=2\Rightarrow f\left(2\right)\approx6,1\)
\(x=0\Rightarrow x^2+1=1\Rightarrow f\left(1\right)=0\)
Từ đó ta phác thảo BBT của \(f\left(x^2+1\right)\) có dạng:

Từ đó ta dễ dàng thấy được pt \(f\left(x^2+1\right)=m\) có nhiều nghiệm nhất khi \(0< m< 6,1\)
\(\Rightarrow\) Có 6 giá trị nguyên của m

1.
\(f\left(x\right)=\dfrac{4}{x}+\dfrac{x-1+1}{1-x}=\dfrac{2^2}{x}+\dfrac{1}{1-x}-1\ge\dfrac{\left(2+1\right)^2}{x+1-x}-1=8\)
\(f\left(x\right)_{min}=8\) khi \(x=\dfrac{2}{3}\)
2.
\(f\left(x\right)=\dfrac{1}{x}+\dfrac{1}{1-x}\ge\dfrac{4}{x+1-x}=4\)
\(f\left(x\right)_{min}=4\) khi \(x=\dfrac{1}{2}\)
f(x)=4x+x−1+11−x=22x+11−x−1≥(2+1)2x+1−x−1=8f(x)=4x+x−1+11−x=22x+11−x−1≥(2+1)2x+1−x−1=8
f(x)min=8f(x)min=8 khi x=23x=23
2.
f(x)=1x+11−x≥4x+1−x=4f(x)=1x+11−x≥4x+1−x=4
f(x)min=4f(x)min=4 khi x=12
Đáp án B
Ta có lim x → 0 + x + 4 - 2 x = lim x → 0 + x + 4 - 2 x + 4 - 2 2 = lim x → 0 + 1 x + 4 + 2 = 1 4
Và lim x → 0 - f x = lim x → 0 - m x + m + 1 4 = m + 1 4
Yêu cầu bài toán lim x → 0 + f ( x ) = lim x → 0 - f ( x ) ⇔ m = 0 .