Đán án C

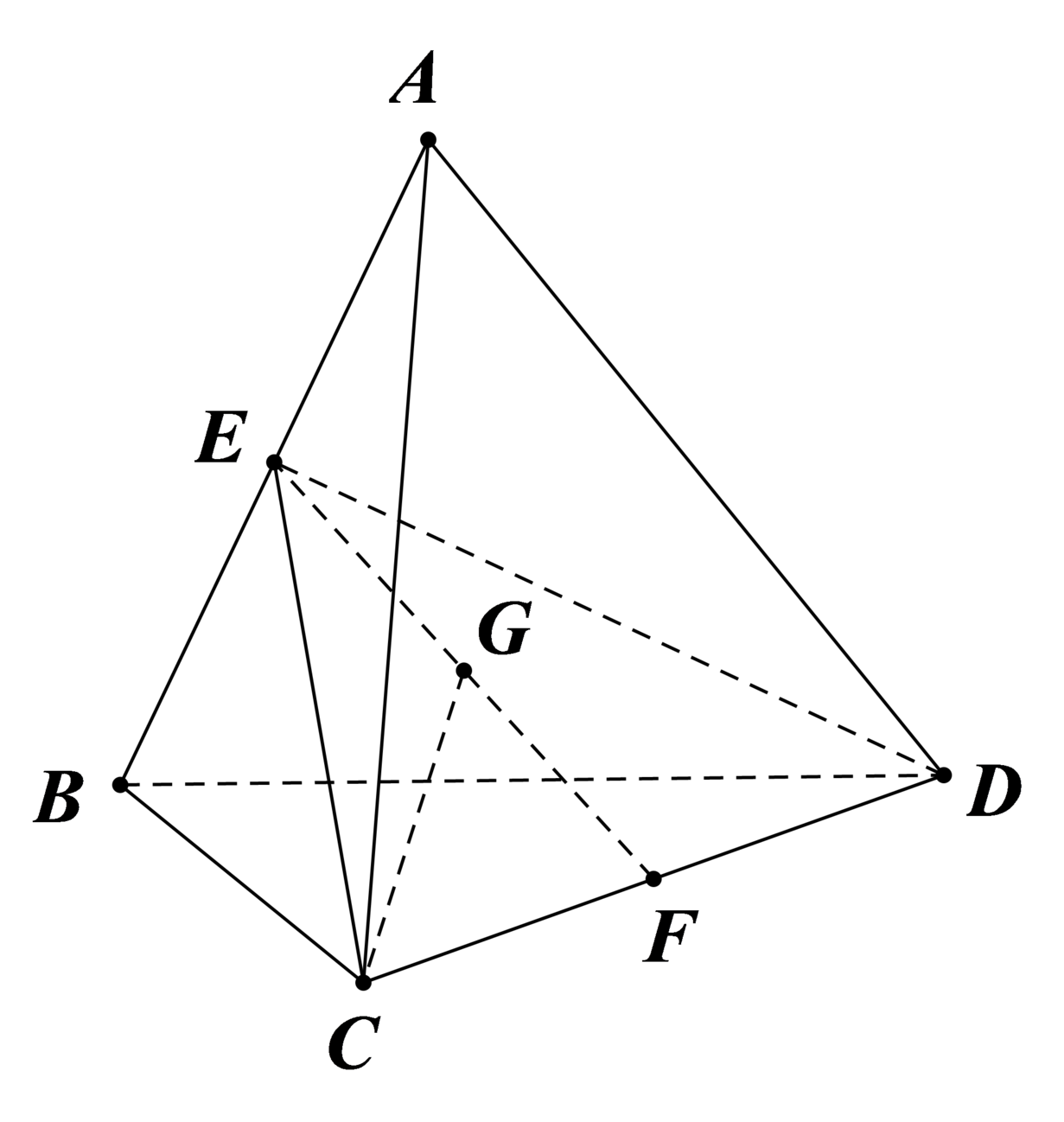
Gọi G là trung điểm của EF thì G chính là tâm mặt cầu ngoại tiếp tứ diện.

Ta có C E 2 = C B 2 + C A 2 2 − A B 2 4 = 6 2 + 6 2 2 − 2 2 4 = 35 ,

E F 2 = C E 2 − C F 2 = 35 − 2 2 = 31

⇒ G F = 31 2 ⇒ R = G C = G F 2 + C F 2 = 31 4 + 4 = 47 2 .

Vậy diện tích mặt cầu cần tính là:

S = 4 π R 2 = 4 π . 47 4 = 47 π .

Đáp án C

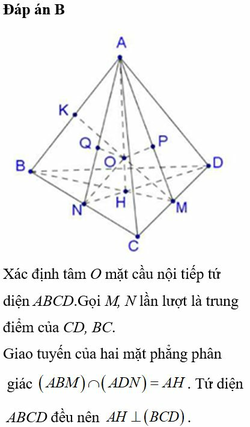
Đặt AB = x, M, N lần lượt là trung điểm AB, CD, I là trung điểm MN thì I là tâm mặt cầu, có 

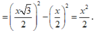
Gọi N, P, Q lần lượt là trung điểm AC, AD, BD thì dễ dàng chứng minh hình thoi MNPQ là thiết diện (việc chứng minh thiết diện là hình thoi cũng vô cùng dễ dàng, 4 cái đường trung bình)

Mặt khác tứ diện đều nên các cặp cạnh đối vuông góc

\(\left\{{}\begin{matrix}AB\perp CD\\AB||MN\\CD||NP\end{matrix}\right.\) \(\Rightarrow MN\perp NP\)

\(\Rightarrow\) Thiết diện là hình vuông cạnh \(\dfrac{a}{2}\)

Chọn B.

Phương pháp:

Ta xác định tâm mặt cầu ngoại tiếp tứ diện ABCD chính là điểm cách đều bốn đỉnh A, B, C, D.

Dựa vào tính chất tam giác cân, hai tam giác bằng nhau, tỉ số lượng giác để chứng minh các đoạn thẳng bằng nhau từ đó tìm được tâm mặt cầu.

Cách giải:

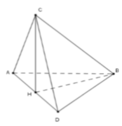
Các tam giác đều ABC và BCD có cạnh 2

⇒ B D = D C = B C = A B = A C = 2  

Nên tam giác CAD cân tại C và  tam giác BAD cân tại B.

Từ (1) và (2) suy ra tam giác CHB vuông cân tại H có cạnh huyền CB = 2.