Cho hai mặt phẳng (P) và (Q) có giao tuyến b và đường thẳng a//b. khẳng định nào dưới đây là sai?
A. Ta có a//(Q) và a//(P)
B. Nếu a ⊂ (Q) thì a//(P)
C. Nếu a ⊂ (P) thì a//(Q)
D. Có thể xảy ra trường hợp a//(Q) đồng thời a//(P)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
23 tháng 8 2023
M thuộc c suy ra M nằm trên mp(Q)
M thuộc a suy ra M nằm trên mp(R)
M cùng thuộc mp(R) và (Q) suy ra M nằm trên giao tuyến của mp(R) và (Q)
Như vậy , M thuộc b.
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 8 2023
– Ta có: a ∩ b = {M}
Mà a ⊂ (P); b ⊂ (Q)
Nên M ∈ (P) và M ∈ (Q)
Do đó M là giao điểm của (P) và (Q).
Mà (P) ∩ (Q) = c, suy ra M ∈ c.
Vậy đường thằng c đi qua điểm M.
– Giả sử trong mặt phẳng (P) có a ∩ c = {N}.
Khi đó N ∈ a mà a ⊂ (R) nên N ∈ (R)
N ∈ c mà c ⊂ (Q) nên N ∈ (Q)
Do đó N là giao điểm của (R) và (Q).
Mà (Q) ∩ (R) = b
CM
23 tháng 8 2018
Chọn D
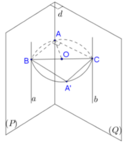
Từ (1) (2) suy ra A thuộc đường tròn đường kính BC bằng 4 không đổi
Do đó d thuộc mặt trụ có khoảng cách giữa đường sinh và trục bằng 2
CM
20 tháng 12 2019
Đáp án D
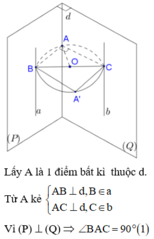
Ta đi chứng minh BC chính là khoảng cách giữa hai đường thẳng a và b, BC = 4:
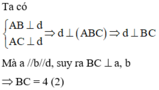
Từ (1) (2) suy ra A thuộc đường tròn đường kính BC bằng 4 không đổi
Do đó d thuộc mặt trụ có khoảng cách giữa đường sinh và trục bằng 2
QT
Quoc Tran Anh Le
Giáo viên
23 tháng 8 2023
a) (Q) cắt (P) theo giao tuyến b suy ra b thuộc (Q).
Do đó a và b không thể chéo nhau.
b) Vì a // (P) và b thuộc (P) suy ra a và b không thể cắt nhau.
Đáp án A