Đáp án D

Theo công thức tính độ tụ  D = 1 f . Về đơn vị thì D có đơn vị điốp (dp) thì tiêu cự phải lấy đơn vị mét (m)

Chọn đáp án D.

Theo công thức tính độ tụ D = 1 f .  Về đơn vị thì D có đơn vị điốp (dp) thì tiêu cự phải lấy đơn vị mét (m).

MÌNH THAM KHẢO NHÉ

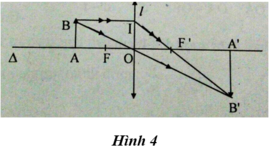
a) Xét △ABO và △A′B′O có: 

ABOˆ=A′B′Oˆ=90⁰

BOAˆ=B′OA′ˆ (hai góc đối đỉnh)

⇒ Hai tam giác ABO và A'B'O là hai tam giác đồng dạng

⇒ \(\frac{A'B'}{AB}=\frac{B'O}{BO}\)

⇒ Độ phóng đại ảnh \(k=\frac{A'B'}{AB}=\frac{h'}{h}=\frac{d'}{d}\)

b) Tương tự: Hai tam giác A'B'F' và IOF' là hai tam giác đồng dạng

⇒\(\text{ }\frac{B'F'}{OF'}=\frac{A'B'}{IO}=\frac{d'}{d}\)

Áp dụng tính chất của tỉ lệ thức: \(\frac{B'F'+OF'}{OF'}=\frac{d'+d}{d}\)hay \(\frac{d'}{f}=\frac{d'+d}{d}\)

⇒\(\frac{1}{f}=\frac{1}{d}=\frac{1}{f'}\)

CÓ MẤY CÁI KÍ HIỆU GÓC, MÌNH KHÔNG BIẾT VIẾT, BẠN THÔNG CẢM

a) Xét \(\Delta ABO\) và \(\Delta A'B'O'\)

\(ABO=A'B'O=90^0\)

\(BOA=B'O'A\)( hai góc đối đỉnh )

\(\Rightarrow\)Hai tam giác ABO và A'B'O là hai tam giác đồng dạng

\(\Rightarrow\frac{A'B}{AB}=\frac{B'O}{BO}\)

\(\Rightarrow\)Độ phóng đại ảnh : \(k=\frac{A'B}{AB}=\frac{h'}{h}=\frac{d'}{d}\)

b) Tương tự : Hai tam giác A'B'F và IOF' là hai tam giác đồng dạng

\(\Rightarrow\frac{B'F'}{OF}=\frac{A'B}{TO}=\frac{d'}{d}\)

Dựa vào tính chất của tỉ lệ thức : \(\frac{B'F'+OF'}{OF'}=\frac{d'+d}{d}\)hay \(\frac{d'}{f}=\frac{d'+d}{d}\)

a) \(\mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{df}}{{d - f}} = \mathop {\lim }\limits_{d \to {f^ + }} \left( {df} \right).\mathop {\lim }\limits_{d \to {f^ + }} \frac{1}{{d - f}}\)

Ta có: \(\mathop {\lim }\limits_{d \to {f^ + }} \left( {df} \right) = f\mathop {\lim }\limits_{d \to {f^ + }} d = {f^2};\mathop {\lim }\limits_{d \to {f^ + }} \frac{1}{{d - f}} =  + \infty \)

\( \Rightarrow \mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{df}}{{d - f}} =  + \infty \)

Ý nghĩa: Khi vật dần đến tiêu điểm từ phía xa thấu kính đến gần thấu kính thì khoảng cách từ ảnh đến thấu kính dần đến \( + \infty \).

b) \(\mathop {\lim }\limits_{d \to  + \infty } g\left( d \right) = \mathop {\lim }\limits_{d \to  + \infty } \frac{{df}}{{d - f}} = \mathop {\lim }\limits_{d \to  + \infty } \frac{{df}}{{d\left( {1 - \frac{f}{d}} \right)}} = \mathop {\lim }\limits_{d \to  + \infty } \frac{f}{{1 - \frac{f}{d}}} = \frac{f}{{1 - 0}} = f\)

Ý nghĩa: Khi khoảng cách từ vật đến thấu kính càng xa thì ảnh tiến dần đến tiêu điểm của ảnh \(\left( {F'} \right)\).

Ta có BI = AO = 2f = 2OF’ => OF’ là đường trung bình của ∆B’BI

=> OB’ = OB => ∆A’B’O = ∆ABO => OA’ = OA = 2f và A’B’ = AB

D = d’ = 2f => d + d’ = 4f => f =(d+d')/4

a) \(D=\dfrac{1}{f}=\dfrac{1}{40}\)

b) Khi d = 20 cm

\(d'=\dfrac{d.f}{d-f}=\dfrac{20.40}{20-40}=-40\left(cm\right)\)

\(k=-\dfrac{d'}{d}=\dfrac{40}{20}=2\)

=> Ảnh ảo, cùng chiều và lớn hơn vật 2  lần.

Đáp án C

Khi 0 < d < f, vật ở trong đoạn FO

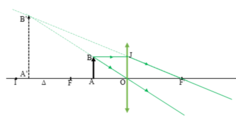
Ảnh là ảo, cùng chiều, lớn hơn vật và nằm ngoài khoảng OF.