Bằng cách biến đổi các hàm số lượng giác, hãy tính: ∫ sin 4 x d x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


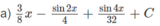
Hướng dẫn:
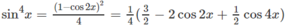
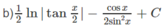
Hướng dẫn: Đặt u = cosx
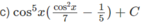
Hướng dẫn: Đặt u = cosx
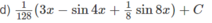
Hướng dẫn:
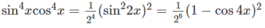

a) \(\sin^4x=\left(\sin^2x\right)^2=\left(\dfrac{1-\cos2x}{2}\right)^2\)
\(=\dfrac{1}{4}\left(1-2\cos2x+\cos^22x\right)\)
\(=\dfrac{1}{4}\left(1-2.\cos2x+\dfrac{1+\cos4x}{2}\right)\)
\(=\dfrac{3}{8}-\dfrac{1}{2}\cos2x+\dfrac{1}{8}\cos4x\)
Vậy:
\(\int\sin^4x\text{dx}=\int\left(\dfrac{3}{8}-\dfrac{1}{2}\cos2x+\dfrac{1}{8}\cos4x\right)\text{dx}\)
\(=\dfrac{3}{8}x-\dfrac{1}{4}\sin2x+\dfrac{1}{32}\sin4x+C\)

a: \(y=f\left(x^2\right)=sin\left(x^2\right)\)
b: \(y=f\left(g\left(x\right)\right)=f\left(x^2\right)=sinx^2\)

Vì 75 ° + 15 ° = 90 ° nên sin 75 ° = cos 15 °
Vì 53 ° + 37 ° = 90 ° nên cos 53 ° = sin 37 °
Vì 47 ° 20 ' + 42 ° 40 ' = 90 ° nên sin 47 ° 20 ' = cos 42 ° 40 '
Vì 62 ° + 28 ° = 90 ° nên tg 62 ° = cotg 28 °
Vì 82 ° 45 ' + 7 ° 15 ' = 90 ° nên cotg 82 ° 45 ' = tg 7 ° 15 '

a) \(\sin \left( {x + h} \right) - \sin x = 2\cos \frac{{2x + h}}{2}.\sin \frac{h}{2}\)
b) Với \({x_0}\) bất kì, ta có:
\(\begin{array}{l}f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\sin x - \sin {x_0}}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \frac{{2\cos \frac{{x + {x_0}}}{2}.\sin \frac{{x - {x_0}}}{2}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\sin \frac{{x - {x_0}}}{2}}}{{\frac{{x - {x_0}}}{2}}}.\mathop {\lim }\limits_{x \to {x_0}} \cos \frac{{x + {x_0}}}{2} = \cos {x_0}\end{array}\)
Vậy hàm số y = sin x có đạo hàm là hàm số \(y' = \cos x\)

\(sin57^0=cos\left(90^0-57^0\right)=cos33^0\)
\(cos43^032'\) ko cần biến đổi vì góc đã thỏa mãn
\(tan72^015'=cot\left(90^0-72^015'\right)=cot\left(17^045'\right)\)
\(cot\left(85^035'\right)=tan\left(90^0-85^035'\right)=tan\left(4^025'\right)\)
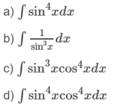
Hướng dẫn: