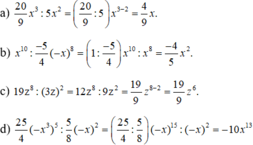
`a, 20x^3y^5 : 5x^2y^2`

`= (20:5)x^(3-2) . y^(5-2)`

`= 4xy^3`

`b, 18x^3y^5 : (3(-x^3)y^2)`

`= -(18:3)y^(5-3)`

`= -6y^2`

\(a,=5^3:5^2=5\\ b,=\left(\dfrac{3}{4}\right)^{5-3}=\left(\dfrac{3}{4}\right)^2=\dfrac{9}{16}\\ c,=1728-512=1216\\ d,=x^{10}:x^8=x^2\\ e,=\left(-x\right)^{5-3}=\left(-x\right)^2=x^2\\ f,=\left(-y\right)^{5-4}=-y\)

a, SBC=\(\sqrt{xy}\)(3\(\sqrt{x}\)-4\(\sqrt{y}\)+5\(\sqrt{xy}\))

câu b bn lmf tương tự nhé,mấy bài này liên quan đến phân tích đa thức bằng nhân tử đó bn:))

\(a,\Rightarrow x\left(x+3\right)-\left(x-3\right)\left(x+3\right)=0\\ \Rightarrow\left(x+3\right)\left(x-x+3\right)=0\\ \Rightarrow3\left(x+3\right)=0\Rightarrow x=-3\\ b,A:B=\left(2x^2-x+4x-2\right):\left(2x-1\right)\\ =\left[x\left(2x-1\right)+2\left(2x-1\right)\right]:\left(2x-1\right)\\ =x+2\)

theo định lí Bơ du ta có

f(x)=f(1)=1\(^{80}\)+\(1^{40}+1^{20}+1^{10}+1^5+1\)=6

Vậy số dư trong phép chia trên là 6

`a, (4x^3y^2 - 8x^2y + 10xy) : 2xy`

`= 2x^2y - 4x + 5`.

`b, 7x^4y^2 - 2x^2y^2 - 5x^3y^4 : 3x^2y`

`= 7/3 x^2y - 3/2y - 5/3xy^3`

1) 1/3 x 1/2 x 3/7 = 3/42 = 1/14

2) 5/4 x 1/3 +1/7 = 5/12 + 1/7 = 35/84 + 12/84 = 47/84

3) 8 x ( 8/9 - 2/3 ) = 8 x 2/9 = 16/9

4) 5/6 x 48/20 x 1/2 = 240/240 = 1

5) ( 2/5 + 3/4 ) + 8 = 23/20 + 8 = 23//20 + 160/20 = 183/20

6) 10 x ( 1/2 - 1/5 ) = 10 x 3/10 = 10/1 x 3/10 = 30/10 = 3

Thực hiện phép chia:

a) (-y^2):y^4=\(\dfrac{-1}{y^2}\)

b) (-x)^5:(-x)^3=(-x)^2

a) (-y²) : y⁴=

b) (-x)⁵ : (-x)³ = (-x)²

a)=1/2 . 8/15 - 3/4.47/9

=4/15 - 47/12

=-73/20

b)=2-1/3 . -21/20

=2+7/20

=47/20

\(a,=\dfrac{5x+30+x^2-30}{x\left(x+6\right)}=\dfrac{x\left(x+5\right)}{x\left(x+6\right)}=\dfrac{x+5}{x+6}\\ b,=\dfrac{3x^2+4x+1-x^2+2x-1-x^2-2x+3}{\left(x-1\right)^2\left(x+1\right)}\\ =\dfrac{x^2+4x+3}{\left(x-1\right)^2\left(x+1\right)}=\dfrac{\left(x+1\right)\left(x+3\right)}{\left(x-1\right)^2\left(x+1\right)}=\dfrac{x+3}{\left(x-1\right)^2}\)

\(c,=\dfrac{3x^2+2x+1+x^2-2x+1-2x^2-2x-2}{\left(x-1\right)\left(x^2+x+1\right)}\\ =\dfrac{2x^2-2x}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{2x\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{2x}{x^2+x+1}\)