Giải các bất phương trình mũ sau: 4 x + 1 > 16
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2 2 x - 2 . 2 x + 8 < 2 3 x . 2 1 - x ⇔ 2 2 x + 2 . 2 x - 8 > 0
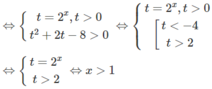

\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)

Đặt t = 3 x (t > 0) , ta có bất phương trình
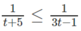
Vì vế trái dương nên vế phải cũng phải dương, tức là 3t - 1 > 0.
Từ đó ta có hệ:
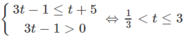
Do đó 1/3 < 3x ≤ 3. Vậy −1 < x ≤ 1.

2 x - 2 > 2 2 x + 1
⇔ |x−2| > 2|x+1|
⇔ x 2 − 4x + 4 > 4( x 2 + 2x + 1)
⇔ 3 x 2 + 12x < 0
⇔ −4 < x < 0

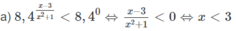
b) 2 x - 2 > 2 2 x + 1
⇔ |x−2| > 2|x+1|
⇔ x 2 − 4x + 4 > 4( x 2 + 2x + 1)
⇔ 3 x 2 + 12x < 0
⇔ −4 < x < 0
c) 2 2 x − 2. 2 x + 8 < 2 3 x . 2 1 - x
⇔ 2 2 x + 2. 2 x − 8 > 0
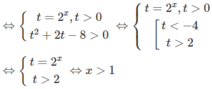
d) Đặt t = 3 x (t > 0) , ta có bất phương trình
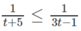
Vì vế trái dương nên vế phải cũng phải dương, tức là 3t - 1 > 0.
Từ đó ta có hệ:
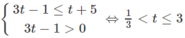
Do đó 1/3 < 3x ≤ 3. Vậy −1 < x ≤ 1.

a) 3 x - 2 < 3 2
⇔ |x − 2| < 2
⇔ −2 < x – 2 < 2
⇔ 0 < x < 4
b) 4 x + 1 > 4 2
⇔ |x + 1| > 2
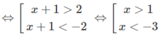
c) 2 - x 2 + 3 x < 2 2
⇔ − x 2 + 3x < 2
⇔ x 2 − 3x + 2 > 0
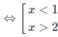
d) 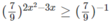
⇔ 2 x 2 − 3x ≤ −1
⇔ 2 x 2 − 3x + 1 ≤ 0 ⇔ 12 ≤ x ≤ 1
e)
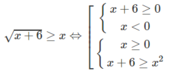
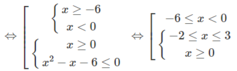
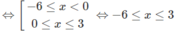
g)
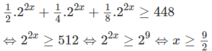
h) Đặt t = 4 x (t > 0), ta có hệ bất phương trình:
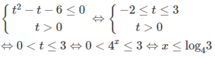
i)
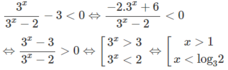
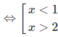
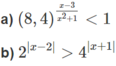
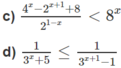
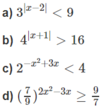
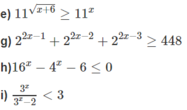
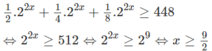
4 x + 1 > 4 2
⇔ |x + 1| > 2