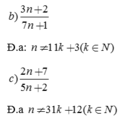
a) Để 21n+4/14n+3 là phân số tổi giản thì ƯCLN(21n+4; 14n+3) =1

Gọi ƯCLN(21n+4; 14n+3) =d => 21n+4 \(⋮\)d; 14n+3 \(⋮\)d

=> (14n+3) -(21n+4) \(⋮\)d

=> 3(14n+3) -2(21n+4) \(⋮\)d

=> 42n+9 - 42n -8 \(⋮\)d

=> 1\(⋮\)d

=> 21n+4/14n+3 là phân số tối giản

Vậy...

c) Gọi ƯC(21n+3; 6n+4) =d; 21n+3/6n+4 =A => 21n+3 \(⋮\)d; 6n+4 \(⋮\)d

=> (6n+4) - (21n+3) \(⋮\)d

=> 7(6n+4) - 2(21n+3) \(⋮\)d

=> 42n +28 - 42n -6\(⋮\)d

=> 22 \(⋮\)cho số nguyên tố d

d \(\in\){11;2}

Nếu phân số A rút gọn được cho số nguyên tố d thì d=2 hoặc d=11

Nếu A có thể rút gọn cho 2 thì 6n+4 luôn luôn chia hết cho 2. 21n+3 chia hết cho 2 nếu n là số lẻ

Nếu A có thể rút gọn cho 11 thì 21n+3 \(⋮\)11 => 22n -n +3\(⋮\)11 => n-3 \(⋮\)11 Đảo lại với n=11k+3 thì 21n+3 và 6n+4 chia hết cho 11

Vậy với n là lẻ hoặc n là chẵn mà n=11k+3 thì phân số đó rút gọn được

mình cũng đang hỏi câu này nè

=1

b1 : 

a, gọi d là ƯC(2n + 1;2n +2) 

=> 2n + 1 chia hết cho d và 2n + 2 chia hết cho d

=> 2n + 2 - 2n - 1 chia hết cho d

=> 1 chia hết cho d

=> d = 1

=> 2n+1/2n+2 là ps tối giản

Bài 1: Với mọi số tự nhiên n, chứng minh các phân số sau là phân số tối giản:

A=2n+1/2n+2

Gọi ƯCLN của chúng là a 

Ta có:2n+1 chia hết cho a

           2n+2 chia hết cho a

- 2n+2 - 2n+1 

- 1 chia hết cho a

- a= 1

  Vậy 2n+1/2n+2 là phân số tối giản

B=2n+3/3n+5

Gọi ƯCLN của chúng là a

2n+3 chia hết cho a

3n+5 chia hết cho a

Suy ra 6n+9 chia hết cho a

            6n+10 chia hết cho a

6n+10-6n+9

1 chia hết cho a 

Vậy 2n+3/3n+5 là phân số tối giản

Mình chỉ biết thế thôi!

#hok_tot#

Câu 1:

gọi n-1/n-2 là M.

Để M là phân số tối giản thì ƯCLN (n - 1; n - 2) = 1 hay -1

Theo đề bài: M = n−1n−2n−1n−2 (n ∈∈Zℤ; n ≠2≠2)

Gọi d = ƯCLN (n - 1; n - 2) 

=> n - 1 - (n - 2) ⋮⋮d       *n - 1 - (n - 2) = n - 1 - n + 2 = n - n + 2 - 1 = 0 + 2 - 1 = 2 - 1 = 1

=> 1 ⋮⋮d

=> d ∈∈Ư (1)

Ư (1) = {1}

=> d = 1

Mà ngay từ lúc đầu d phải bằng 1 rồi.

Vậy nên với mọi n ∈∈Z và n ≠2≠2thì M là phân số tối giản.

umk đây này

Phân số đã cho có dạng: a/2+a+n với a=1,2,3,...,2004.

UCLN(a;2+a+n)=1 do đó a;2+a+n nguyên tố cùng nhau. Do vậy 2+n là số nguyên tố với n nhỏ nhất

Do đó 2+n=2003 (Vì 2003 là số nguyên tố)

Vậy n=2001

Phân số đã cho có dạng: \(\frac{a}{2+a+n}\) với a=1,2,3,...,2004.

UCLN(a;2+a+n)=1 do đó a;2+a+n nguyên tố cùng nhau.

Do vậy 2+n là số nguyên tố với n nhỏ nhất

Do đó 2+n=2003 (Vì 2003 là số nguyên tố)

Vậy n=2001

n =2001 đấy bạn ạ 

a) để 2n+3/4n+1 là phân số tối giản thì ta đi chứng minh 2n+3 và 4n+1 là nguyên tố cùng nhau .

=>UCLN ( 2n+3;4n+1 ) = d

ta có : 2n+1 chia hết cho d

          4n+1 chia hết cho d

=>      2(2n+1) chia hết cho d

          4n+1 chia hết cho d 

=> 4n+2 chia hết cho d  

     4n+1 chia hết cho d 

=>     [( 4n+2)-(4n+1)] chia hết cho d

=>      1 chia hết cho d 

=>     d = 1

=> ucln ( 2n+3; 4n+1)=1

vì ucln ( 2n+3;4n+1)=1 nên 2n+3=1;4n+1=1 

                                         2n=1-3   4n=1-1

                                         2n=-2    4n=0

                                           n=-1(loại)  n=0 ( chọn)

vậy để 2n+3/4n+1 là phân số tối giản thì n=0

tớ nghĩ thế ko biết có đúng ko !

nhưng nếu cảm thấy đúng thì nhớ tk cho tớ nhé 

mấy phần còn lại thì các bạn cứ làm như phần a nhé !

Câu 11. Không khí nóng nhẹ hơn không khí lạnh vì

          A. khối lượng riêng của không khí nóng nhỏ hơn.

          B. khối lượng của không khí nóng nhỏ hơn.

          C. khối lượng của không khí nóng lớn hơn.

          D. khối lượng riêng của không khí nóng lớn hơn.

Câu hỏi của Đỗ Quynhg Anh - Toán lớp 7 - Học toán với OnlineMath

Bạn tham khảo bài nhé !!!

oke, mình cảm ơn nhé