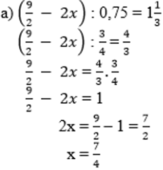
e: ta có: \(4x^2+4x-6=2\)

\(\Leftrightarrow4x^2+4x-8=0\)

\(\Leftrightarrow\left(x+2\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)

f: Ta có: \(2x^2+7x+3=0\)

\(\Leftrightarrow\left(x+3\right)\left(2x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-\dfrac{1}{2}\end{matrix}\right.\)

a) ${\left(2x-1\right)}^2-25=0$

${\left(2x-1\right)}^2=0+25=25$

${\left(2x-1\right)}^2=5^2={\left(-5\right)}^2$

$\Rightarrow [\begin{array}{c}2x-1=5\\ 2x-1=-5\end{array}\Rightarrow [\begin{array}{c}2x=6\\ 2x=-4\end{array}\Rightarrow [\begin{array}{c}x=3\\ x=-2\end{array}$

b) $8x^3-50x=0$

$2x(4x^2$

câu b thiếu bn ơi

a: Ta có: \(\left(2x-1\right)^2-25=0\)

\(\Leftrightarrow\left(2x-6\right)\left(2x+4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)

a) \(\left(2\dfrac{3}{4}-1\dfrac{4}{5}\right)\cdot x=1\)

\(\left(\dfrac{11}{4}-\dfrac{9}{5}\right)\cdot x=1\)

\(\dfrac{19}{20}x=1\)

\(x=\dfrac{20}{19}\)

Vậy \(x=\dfrac{20}{19}\)

b) \(\left(x^2-9\right)\left(3-5x\right)=0\)

TH1:

\(x^2-9=0\)

\(x^2=9\)

\(x^2=3^2=\left(-3\right)^2\)

=>\(x\in\left\{3;-3\right\}\)

TH2:

\(3-5x=0\)

\(5x=3\)

\(x=\dfrac{3}{5}\)

Vậy \(x\in\left\{3;-3;\dfrac{3}{5}\right\}\)

mọi người ơi giúp mk đi mk dốt toán lém

Bài 1: 

a: Số phần tử của tập hợp A là:

50-11+1=40

b: Số phần tử của tập hợp B là:

\(\left(100-0\right):10+1=11\)

c: Tập hợp C có 1 phần tử

d: Tập hợp D có : \(\left(31-5\right):2+1=14\)

e: Tập hợp E có 5 phần tử

f: Tập hợp F có vô số phần tử

a: =>2x^2=4

=>x^2=2

=>\(x=\pm\sqrt{2}\)

b: =>(x+1)^2-4=0

=>(x+1+2)(x+1-2)=0

=>(x+3)(x-1)=0

=>x=1 hoặc x=-3

c: =>(2x-1)^2-3^2=0

=>(2x-1-3)(2x-1+3)=0

=>(2x-4)(2x+2)=0

=>x=2 hoặc x=-1

d: x^2-x=0

=>x(x-1)=0

=>x=0 hoặc x=1

`a)sqrt{x^2-2x+1}=2`

`<=>sqrt{(x-1)^2}=2`

`<=>|x-1|=2`

`**x-1=2<=>x=3`

`**x-1=-1<=>x=-1`.

Vậy `S={3,-1}`

`b)sqrt{x^2-1}=x`

Điều kiện:\(\begin{cases}x^2-1 \ge 0\\x \ge 0\\\end{cases}\)

`<=>` \(\begin{cases}x^2 \ge 1\\x \ge 0\\\end{cases}\)

`<=>x>=1`

`pt<=>x^2-1=x^2`

`<=>-1=0` vô lý

Vậy pt vô nghiệm

`c)sqrt{4x-20}+3sqrt{(x-5)/9}-1/3sqrt{9x-45}=4(x>=5)`

`pt<=>sqrt{4(x-5)}+sqrt{9*(x-5)/9}-sqrt{(9x-45)*1/9}=4`

`<=>2sqrt{x-5}+sqrt{x-5}-sqrt{x-5}=4`

`<=>2sqrt{x-5}=4`

`<=>sqrt{x-5}=2`

`<=>x-5=4`

`<=>x=9(tmđk)`

Vậy `S={9}.`

`d)x-5sqrt{x-2}=-2(x>=2)`

`<=>x-2-5sqrt{x-2}+4=0`

Đặt `a=sqrt{x-2}`

`pt<=>a^2-5a+4=0`

`<=>a_1=1,a_2=4`

`<=>sqrt{x-2}=1,sqrt{x-2}=4`

`<=>x_1=3,x_2=18`,

`e)2x-3sqrt{2x-1}-5=0`

`<=>2x-1-3sqrt{2x-1}-4=0`

Đặt `a=sqrt{2x-1}(a>=0)`

`pt<=>a^2-3a-4=0`

`a-b+c=0`

`<=>a_1=-1(l),a_2=4(tm)`

`<=>sqrt{2x-1}=4`

`<=>2x-1=16`

`<=>x=17/2(tm)`

Vậy `S={17/2}`

d.

ĐKXĐ: $x\geq 2$. Đặt $\sqrt{x-2}=a(a\geq 0)$ thì pt trở thành:

$a^2+2-5a=-2$

$\Leftrightarrow a^2-5a+4=0$

$\Leftrightarrow (a-1)(a-4)=0$

$\Rightarrow a=1$ hoặc $a=4$

$\Leftrightarrow \sqrt{x-2}=1$ hoặc $\sqrt{x-2}=4$

$\Leftrightarrow x=3$ hoặc $x=18$ (đều thỏa mãn)

e. ĐKXĐ: $x\geq \frac{1}{2}$

Đặt $\sqrt{2x-1}=a(a\geq 0)$ thì pt trở thành:

$a^2+1-3a-5=0$

$\Leftrightarrow a^2-3a-4=0$

$\Leftrightarrow (a+1)(a-4)=0$

Vì $a\geq 0$ nên $a=4$

$\Leftrightarrow \sqrt{2x-1}=4$

$\Leftrightarrow x=\frac{17}{2}$

a: \(\Leftrightarrow\left|2x-3\right|=7\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-3=7\\2x-3=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-2\end{matrix}\right.\)

a, \(\sqrt{\left(2x-3\right)^2}=7\\ \Rightarrow\left|2x-3\right|=7\\ \Rightarrow\left[{}\begin{matrix}2x-3=7\\2x-3=-7\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=5\\x=-2\end{matrix}\right.\)

c, \(\sqrt{x^2-9}-3\sqrt{x-3}=0\\ \Rightarrow\sqrt{x-3}\sqrt{x+3}-3\sqrt{x-3}=0\\ \Rightarrow\sqrt{x-3}\left(\sqrt{x+3}-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}\sqrt{x-3}=0\\\sqrt{x+3}-3=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x-3=0\\x+3=9\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=6\left(tm\right)\end{matrix}\right.\)