Một vật nhỏ dao động điều hòa dọc theo trục Ox với biên độ 8cm, chu kỳ 2s. Tại thời điểm t = 0, vật đi qua vị trí cân bằng ngược chiều dương. Hãy viết phương trình dao động của vật?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
21 tháng 11 2017
Đáp án C
Phương pháp: Sử dụng lí thuyết đại cương về dao động điều hòa
Cách giải:
Biên độ: A = 5cm
Tần số góc: ω = π rad/s.
Tại t = 0, vật qua VTCB theo chiều dương: φ = - π/2 (rad)
=> x = 5cos(πt – π/2) cm
VT
7 tháng 10 2019
Chọn D
A=5cm
T=2s=> w=p Rad/s
t=0s thì x=0 và vật đi qua vị trí cân bằng theo chiều dương =>j = - p/2
VT
4 tháng 8 2019
Đáp án là D
A=5cm
T=2s=> w=p Rad/s
t=0s thì x=0 và vật đi qua vị trí cân bằng theo chiều dương =>j = - p/2
VT
14 tháng 5 2018
ta có: A = 5 cm, T = 2s
→ ω = π rad / s
Tại t = 0, vật đi qua vị trí cân bằng theo chiều dương → φ = - 0 , 5 π
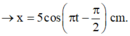
Đáp án B
VT
23 tháng 3 2017
Đáp án B
+ Ta có A=5cm T = 2 s → ω = π r a d / s
Tại t=0, vật đi qua vị trí cân bằng theo chiều dương → φ 0 = - 0 , 5 π
→ x = 5 cos π t - π 2 c m .
VT
15 tháng 3 2019
Đáp án A
Phương trình dao động của vật x = 5 cos π t + π 2 cm
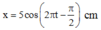
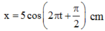
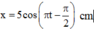
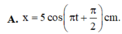
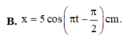
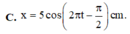
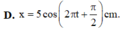
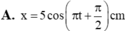
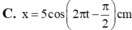
\(T=2s\)
Ta có: \(L=2A=8cm\Rightarrow A=4cm\)
Tần số góc: \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{2}=\pi\)(rad/s)
Tại \(t=0\): \(\Rightarrow\left\{{}\begin{matrix}x=Acos\varphi=0\\v=-A\omega sin\varphi>0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}cos\varphi=0\\sin\varphi< 0\end{matrix}\right.\)\(\Rightarrow\varphi=-\dfrac{\pi}{2}\)
Phương trình dao động của vật:
\(x=4cos\left(\pi t-\dfrac{\pi}{2}\right)\)