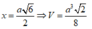Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy, góc S B C ^ = 60 0 . Tính theo a thể tích khối chóp .
A . a 3 2 4
B . a 3 2 24
C . a 3 3 4
D . a 3 2 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
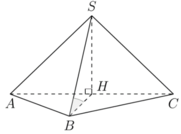
Gọi H là trung điểm AC. Ta có tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với (ABC)
suy ra S H ⊥ A B C
Ta có
S B , A B C = S B H ^ = 45 o ⇒ S H = B H = 1 2 A C = a 2 2 V S . A B C = 1 3 . a 2 2 . 1 2 a 2 = a 3 2 12

a) Tính \(V_{S.ABM}\)
Tam giác ABC cân tại A , SBC cân tại S \(\Rightarrow AM\perp BC;SM\perp BC\) tại M
Vì mp(SBC) vuông góc với mặt đáy suy ra SM vuông góc với mặt đáy
Góc giữa SB và mặt đáy là góc SBM=300
\(\Rightarrow SM=BMtan.\widehat{SBM}=\frac{a}{2}.tan30^0=\frac{a}{2\sqrt{3}}\)
\(\Rightarrow V_{S.ABM}=\frac{1}{3}.SM.S_{ABM}=\frac{1}{3}.\frac{a}{2\sqrt{3}}.\frac{1}{2}.\frac{a}{2}.\frac{a\sqrt{3}}{2}=\frac{a^3}{48}\)
b) Tính k/c SB và AM
Kẻ MH vuông góc với SB tại H
Dễ dàng chứng minh MH là đoạn vuông góc chung giữa SB và AM
Vậy khảong cách giữa SB và AM bằng đoạn MH và bằng \(\frac{BM}{cos.\widehat{HBM}}=\frac{\frac{a}{2}}{cos30^0}=\frac{a}{\sqrt{3}}\)

Đáp án A
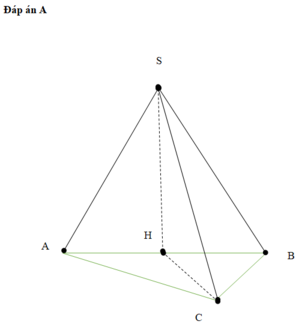
Xét ∆SAB, ta có: SA = SB = a 2 2
ð SH = a 2
Vậy V S . A B C = 1 3 . a 2 . S A B C = 1 3 . a 2 . 1 2 3 2 . a . a = a 3 3 24
Đáp án D.
Đặt SH = x, tính SB, SC theo x. Sau đó áp dụng định lí cosin cho ∆ SBC
Tìm được