Đáp án A.

Vì A ’ A = A ’ B = A ’ C ⇒ A ' . A B C  là hình chóp tam giác đều.

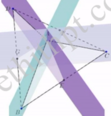
Hình vẽ minh họa: Hình chóp tam giác đều ABCD có 3 mặt phẳng đối xứng.

Vậy hình chóp tam giác đều (không phải tứ diện đều) có 3 mặt phẳng đối xứng.

Đáp án C

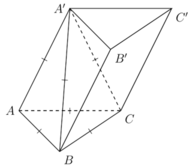
Từ giả thiết suy ra tứ diện A'ABC đều có cạnh a nên có thể tích là

V A ' A B C = a 3 2 12

Khi đó

V A B C . A ' B ' C ' = d A ' , A B C . S A B C = 3 V A ' A B C = a 3 2 4

Đáp án B

Gọi M là trung điểm BC

Vì các cạnh AA’ = A’B = A’C

    => Hình chiếu của A’ trên (ABC) là tâm đường tròn ngoại tiếp ∆ABC

    => A’M ⊥ (ABC)

Xét ∆A’BC, ta có A'M = a 3

Xét ∆ABC, ta có: AB = AC = a 2

Vậy 

Đáp án B

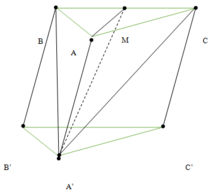
Gọi M là trung điểm BC

Vì các cạnh AA’ = A’B = A’C

ð Hình chiếu của A’ trên (ABC) là tâm đường tròn ngoại tiếp ∆ABC

ð A’M ⊥  (ABC)

Xét ∆A’BC, ta có: A’M =   a 3

Xét ∆ABC, ta có: AB = AC =   a 2

Vậy

V A B C . A ' B ' C ' = a 3 . S A B C = a 3 . 1 2 . a 2 . a 2 = a 3 3  

Đáp án C

Gọi M là trung điểm của BC suy ra 

Lại có 

Đáp án A

Gọi I là giao điểm của AH và BC

Theo giả thiết H là trực tâm của tam giác đều ABC nên AH là đường cao và H cũng lả trọng tâm của tam giác đều ABC

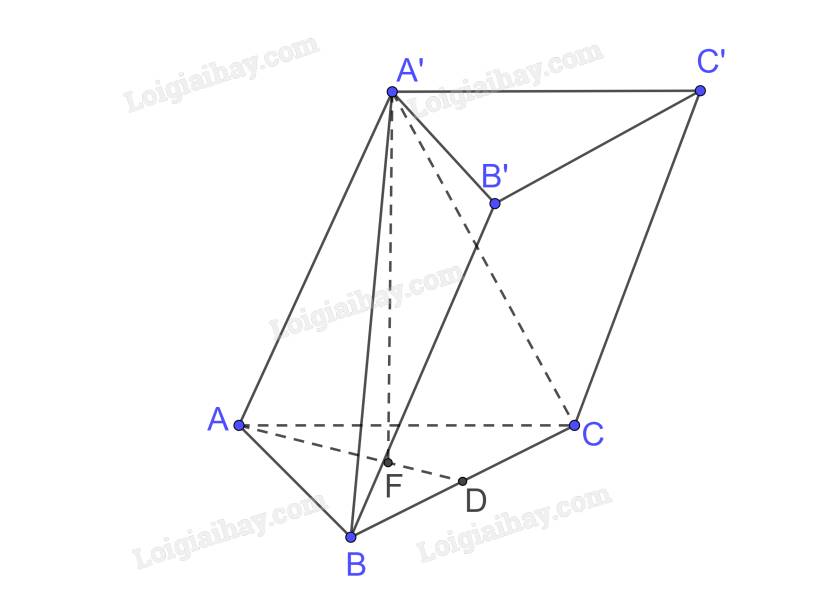
Vì hình chóp A’.ABC có A'A = A'B = A'C và đáy ABC là tam giác đều nên hình chóp A’.ABC đều.

Gọi F là hình chiếu của A’ trên (ABC) nên F là tâm của đáy ABC là tam giác đều do đó F cũng là trọng tâm của tam giác ABC.

Gọi AF cắt BC tại D

Tam giác ABC đều cạnh a nên \(AD = \frac{{a\sqrt 3 }}{2}\)

Mà F là trọng tâm nên \(AF = \frac{2}{3}AD = \frac{{a\sqrt 3 }}{3}\)

Xét tam giác A’AF vuông tại F có

\(A'F = \sqrt {A'{A^2} - A{F^2}}  = \sqrt {{b^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}}  = \sqrt {{b^2} - \frac{{{a^2}}}{3}} \)

Diện tích tam giác đều ABC là \(S = \frac{{{a^2}\sqrt 3 }}{4}\)

Thể tích khối lăng trụ là \(V = A'F.S = \sqrt {{b^2} - \frac{{{a^2}}}{3}} .\frac{{{a^2}\sqrt 3 }}{4}\)