Xét tổng quát cơ năng của vật tại vị trí động năng bằng n thế năng là:

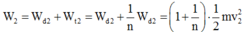
Do vật rơi tự do tức là vật chỉ chịu tác dụng của trọng lực, thì cơ năng của vật là một đại lượng bảo toàn tức là

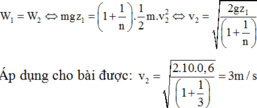
Chọn g= 10 m/s²

Theo đề ta có 

\(3W_đ=W_t\)

Độ cao vật có thế năng bằng 3 lần động năng so với mặt đất là

\(h'=\dfrac{W_t}{mg}=\dfrac{3W_đ}{mg}=\dfrac{3\cdot\dfrac{1}{2}\cdot m\cdot v^2}{mg}=\dfrac{\dfrac{3}{2}\cdot2\cdot g\cdot\left(h-h'\right)}{g}=3h-3h'\)

\(\Rightarrow h'=\dfrac{3}{4}h=33,75\left(m\right)\)

Vận tốc của vật tại đó thế năng bằng 3 lần động năng là

\(3\cdot W_đ=W_t\Leftrightarrow\dfrac{3}{2}\cdot m\cdot v^2=mgh'\Leftrightarrow v^2=\dfrac{h'\cdot g}{\dfrac{3}{2}}=225\)

\(\Rightarrow v=15\left(\dfrac{m}{s}\right)\)

`@W_t=mgz=2.10.2=40(J)`

   `W_đ=1/2mv^2=1/2 .2.0^2=0(J)`

  `W=W_t+W_đ=40+0=40(J)`

`@W_[(W_đ=2W_t)]=W_[đ(W_đ=2W_t)]+W_[t(W_đ=2W_t)]=40`

    Mà `W_[đ(W_đ=2W_t)]=2W_[t(W_đ=2W_t)]`

   `=>3W_[t(W_đ=2W_t)]=40`

`<=>3mgz_[(W_đ=2W_t)]=40`

`<=>3.2.10.z_[(W_đ=2W_t)]=40`

`<=>z_[(W_đ=2W_t)]~~0,67(m)`

`@W_[đ(max)]=W_[t(max)]=40`

`<=>1/2mv_[max] ^2=40`

`<=>1/2 .2v_[max] ^2=40`

`<=>v_[max]=2\sqrt{10}(m//s)`

Sao lại 3 lần thế năng? Trong khi đó có 2? giải thích giúp em.

Vật được thả rơi tự do => Cơ năng được bảo toàn.
Chọn mốc thế năng tại mặt đất.
Gọi vị trí vật được thả rơi tự do là A, khi đó vA = 0 (m/s) => WđA = 0
Gọi vị trí vật có Wđ=1/3W là B
WA=WB = WđA + WtA = m.g.hA=m.10.60 = 600m
WđB = 1/3 WB
=> WđB = 1/3.600m = 200m
<=> 1/2.m.vB^2 = 200m
<=> vB = 20 (m/s)
Khi đó hB = 40 (m) (Thay vào công thức là ra nhé)

Vật được thả rơi tự do => Cơ năng được bảo toàn.
Chọn mốc thế năng tại mặt đất.
Gọi vị trí vật được thả rơi tự do là A, khi đó vA = 0 (m/s) => WđA = 0
Gọi vị trí vật có Wđ=1/3W là B
WA=WB = WđA + WtA = m.g.hA=m.10.60 = 600m
WđB = 1/3 WB
=> WđB = 1/3.600m = 200m
<=> 1/2.m.vB^2 = 200m
<=> vB = 20 (m/s)
Khi đó hB = 40 (m) (Thay vào công thức là ra nhé)

1) Chọn mốc thế năng tại mặt đất, bỏ qua lực cản => Cơ năng được bảo toàn.
Gọi vị trí tại mặt đất là A.
Vị trí thả vật là B
Vị trí vật có động năng gấp 2 lần thế năng là C.
Vị trí vật có độ cao so với mặt đất là 3m là D.
a) + W_B = Wđ_B + Wt_B = \(\dfrac{1}{2}\).m.v_B² + m.g.h_B
= 0,5.10.10 = 50 (J) (Do v_B = 0)
+ Ta có:W_B = W_A = Wđ_A = 50(J) (Do Wt_A = 0)
b) + Wđ_c = 2Wt_c
<=> \(\dfrac{1}{2}\).m.v_C² = 2.m.g.h_C
+ W_C = W_A = 50
<=> \(\dfrac{1}{2}\).m.v_C² + m.g.h_C = 50
<=> 2.m.g.h_C + m.g.h_C = 50
<=> 3.m.g.h_C = 50
<=> 3.0,5.10.h_C = 50
<=> h_C = \(\dfrac{10}{3}\)(m) ≃ 3,33 (m)
c) W_D = W_A = 50
<=> Wđ_D + Wt_D = 50
<=> \(\dfrac{1}{2}\).m.v_D² + m.g.h_D = 50
<=> \(\dfrac{1}{2}\).0,5.v_D² + 0,5.10.3 = 50
<=> v_D = 2\(\sqrt{35}\)(m/s) ≃ 11,83 (m/s)

2) Chọn mốc thế năng tại vị trí O phía trên mặt đất 1m
Khi đó, Wt_B = m.g.h_B = 0,5.10.(10-1) = 45 (J)
Wt_A = m.g.h_A = 0,5.10.(-1) = -5 (J)

a,

\(W_t=m\cdot g\cdot z=2\cdot10\cdot100=2000J\)

b,

Áp dụng ĐLBTCN :

\(W=W_1\\ \Leftrightarrow\dfrac{1}{2}\cdot m\cdot V^2+m\cdot g\cdot z=\dfrac{1}{2}\cdot m\cdot V_1+m\cdot g\cdot z_1^2\\ \Leftrightarrow m\cdot g\cdot z=\dfrac{1}{2}\cdot m\cdot V_1^2\\ \Leftrightarrow2000=\dfrac{1}{2}\cdot2\cdot V_1^2\\ \Leftrightarrow V_1=20\sqrt{5}\)

c,

Ta có:

\(W_{t_{30}}=m\cdot g\cdot30=2\cdot10\cdot30=600J\)

\(V_{30}=\sqrt{2\cdot g\cdot S}=\sqrt{2\cdot10\cdot70}=10\sqrt{14}\) m/s

\(W_{đ_{30}}=\dfrac{1}{2}\cdot2\cdot V_{30}^2=\dfrac{1}{2}\cdot2\cdot\left(10\sqrt{14}\right)^2=1400J\)

Tại sao W=W1 vậy ạ