Xét tính đúng sai của mỗi mệnh đề sau và phát biểu mệnh đề phủ định của nó: √2 là một số hữu tỉ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
+) Mệnh đề phủ định của mệnh đề P là \(\overline P \): “5,15 không phải là một số hữu tỉ”
Mệnh đề P đúng, \(\overline P \) sai vì \(5,15 = \frac{{103}}{{20}} \in \mathbb{Q}\), là một số hữu tỉ.
+) Mệnh đề phủ định của mệnh đề Q là \(\overline Q \): “2 023 không phải là số chẵn” (hoặc “2 023 là số lẻ”)
Mệnh đề Q sai, \(\overline Q \) đúng vì 2 023 có chữ số tận cùng là \(3 \ne \left\{ {0;2;4;6;8} \right\}\), đo đó 2 023 không phải là số chẵn.
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
23 tháng 9 2023
P: đúng
phủ định: "5,15 không phải số hữu tỉ"
Q: sai
Phủ định: "1023 không phải số chẵn"
PT
1
CM
28 tháng 8 2018
Mệnh đề π < 3, 15 đúng vì π = 3,141592654…
Mệnh đề phủ định: "π ≥ 3, 15"
PT
1
CM
28 tháng 3 2019
Mệnh đề ‘’|–125| ≤ 0’’ sai vì |–125| = 125 > 0
Mệnh đề phủ định: "|–125| > 0"
PT
1
CM
5 tháng 4 2018
Mệnh đề « 1794 chia hết cho 3 » đúng vì 1794 : 3 = 598
Mệnh đề phủ định: "1794 không chia hết cho 3"
17 tháng 5 2017
a) \(\left(P\Rightarrow Q\right):\)"Nếu \(x\) là một số hữu tỉ \(x^2\) cũng là một số hữu tỉ". Mệnh đề đúng.
b) Mệnh đề đảo là " Nếu \(x^2\) là một số hữu tỉ thì \(x\) là một số hữu tỉ"
c) Chẳng hạn, với \(x=\sqrt{2}\) mệnh đề này sai
PT
1
mệnh đề này đúng.
PT
1
CM
20 tháng 3 2019
Mệnh đề sai.
Phủ định là "x = 2 không là nghiệm của phương trình"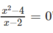 
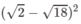
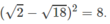
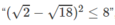mệnh đề này đúng.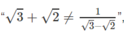
Mệnh đề “√2 là số hữu tỉ’’ sai vì √2 là số vô tỉ
Mệnh đề phủ định: "√2 không phải là một số hữu tỉ"