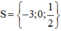Giải phương trình sau bằng cách đưa về phương trình tích: 2x3 + 5x2 – 3x = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3x3 - 3x2- 6x = 0
x ( 3x2 - 3x - 6 ) = 0
x [ 3x2 + 3x - 6x - 6 ] = 0
x [ 3x ( x + 1 ) - 6 ( x + 1 ) ] = 0
x ( 3x - 6 ) ( x + 1 ) = 0
<=> x = 0 hoặc 3x - 6 = 0 hoặc x + 1 = 0
1) x = 0
2) 3x - 6 = 0 <=> x = 2
3) x + 1 = 0 <=> x = -1
Vậy taaph nghiệm của phương trình đã cho S={0 : -1 : 2 }
\(3x^3-3x^2-6x=0\)
\(3x^3-6x^2+3x^2-6x=0\)
\(3x^2.\left(x-2\right)+3x\left(x-2\right)=0\)
\(\left(3x^2+3x\right)\left(x-2\right)=0\)
\(3x\left(x+1\right)\left(x-2\right)=0\)
\(\Rightarrow3x=0\) \(\Rightarrow x=0\)hoặc \(\orbr{\begin{cases}x+1=0\\x-2=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=-1\\x=2\end{cases}}\)

x 2 – 3x + 2 = 0 ⇔ x 2 – x – 2x + 2 = 0
⇔ x(x – 1) – 2(x – 1) = 0 ⇔ (x – 2)(x – 1) = 0
⇔ x – 2 = 0 hoặc x – 1 = 0
x – 2 = 0 ⇔ x = 2
x – 1 = 0 ⇔ x = 1
Vậy phương trình có nghiệm x= 2 hoặc x = 1

⇔ [( x 2 +x +1) + (4x -1 )] [( x 2 +x +1) - (4x -1 )]=0
∆ = - 3 2 -4.2.1 = 9 -8 =1 > 0
∆ = 1 =1
x 2 + 3 x + 2 2 = 6.( x 2 +3x +2)
⇔ x 2 + 3 x + 2 2 - 6.( x 2 +3x +2)=0
⇔ ( x 2 +3x + 2)[ ( x 2 +3x + 2) -6] =0
⇔ ( x 2 +3x + 2) .( x 2 +3x -4 )=0
x 2 +3x + 2 =0
Phương trình có dạng a –b +c =0 nên x 1 = -1 , x 2 =-2
x 2 +3x -4 =0
Phương trình có dạng a +b +c =0 nên x 1 = 1 , x 2 = -4
Vậy phương trình đã cho có 4 nghiệm :
x 1 = -1 , x 2 =-2 ; x 3 = 1 , x 4 =-4

4x2 – 1 = (2x + 1)(3x – 5)
⇔ 4x2 – 1 – (2x + 1)(3x – 5) = 0
⇔ (2x – 1)(2x + 1) – (2x + 1)(3x – 5) = 0
⇔ (2x + 1)[(2x – 1) – (3x – 5)] = 0
⇔ (2x + 1)(2x – 1 – 3x + 5) = 0
⇔ (2x + 1)(4 – x) = 0
⇔ 2x + 1= 0 hoặc 4 – x = 0
+ 2x + 1 = 0 ⇔ 2x = -1 ⇔ x = -1/2.
+ 4 – x = 0 ⇔ x = 4.
Vậy phương trình có tập nghiệm 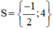

(2x + 1)(3x – 2) = (5x – 8)(2x + 1)
⇔ (2x + 1)(3x – 2) – (5x – 8)(2x + 1) = 0
⇔ (2x + 1).[(3x – 2) – (5x – 8)] = 0
⇔ (2x + 1).(3x – 2 – 5x + 8) = 0
⇔ (2x + 1)(6 – 2x) = 0
⇔ 2x + 1 = 0 hoặc 6 – 2x = 0
+ 2x + 1 = 0 ⇔ 2x = -1 ⇔ x = -1/2.
+ 6 – 2x = 0 ⇔ 6 = 2x ⇔ x = 3.
Vậy phương trình có tập nghiệm 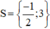

x3 + 3x2 + 2x = 0 ⇔ x(x2 + 3x + 2) = 0
⇔ x = 0 hoặc x2 + 3x + 2 = 0 (1)
Giải phương trình (1) ta được các nghiệm x = -1; x = -2
Vậy phương trình đã cho có 3 nghiệm x = 0; x = -1; x = -2

x 3 + 3 x 2 + 2 x = 0 ⇔ x ( x 2 + 3 x + 2 ) = 0
⇔ x = 0 hoặc x 2 + 3 x + 2 = 0 ( 1 )
Giải phương trình (1) ta được các nghiệm x = -1; x = -2
Vậy phương trình đã cho có 3 nghiệm x = 0; x = -1; x = -2

Ta có: x 3 – 5 x 2 –x +5 = 0 ⇔ x 2 ( x -5) – ( x -5) =0
⇔ (x -5)(x2 -1) =0 ⇔ (x -5)(x -1)(x +1) =0
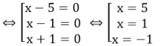
Vậy phương trình đã cho có 3 nghiệm :x1 = 5;x2 =1;x3=-1

Ta có: 3 x 3 +6 x 2 -4x =0 ⇔ x(3 x 2 +6x -4) =0
⇔ x = 0 hoặc 3 x 2 +6x -4 =0
Giải phương trình 3 x 2 +6x -4 =0
∆ ’ = 3 2 - 3(-4) = 9 + 12 = 21 > 0
∆ ' = 21
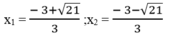
Vậy phương trình đã cho có 3 nghiệm
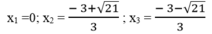
2x3 + 5x2 – 3x = 0
⇔ x(2x2 + 5x – 3) = 0
⇔ x.(2x2 + 6x – x – 3) = 0
⇔ x. [2x(x + 3) – (x + 3)] = 0
⇔ x.(2x – 1)(x + 3) = 0
⇔ x = 0 hoặc 2x – 1 = 0 hoặc x + 3 = 0
+ 2x – 1 = 0 ⇔ 2x = 1 ⇔ x = 1/2.
+ x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm