Cho phương trình 4x -( m + 3) 2x + m + 2 = 0 (m là tham số thực dương) có hai nghiệm thực phân biệt thỏa mãn x 1 2 + x 2 2 = 9 . Mệnh đề nào dưới đây là đúng ?
A. 1< m < 3
B. 3 < m < 5
C. 0 < m < 1
D. m > 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
ta có m 4 − m 2 + 1 = m 2 − 1 2 2 + 3 4 ≥ 3 4 ∀ m
1 5 x 2 − 4 x + 3 = m 4 − m 2 + 1 ⇔ x 2 − 4 x + 3 = − log 4 m 4 − m 2 + 1
Xét hàm số y = x 2 − 4 x + 3 có bảng biến thiên:
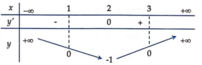
Suy ra bảng biến thiên của hàm số y = x 2 − 4 x + 3 :
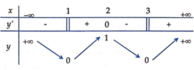
Phương trình x 2 − 4 x + 3 = − log 5 m 4 − m 2 + 1 có 4 nghiệm phân biệt
⇔ 0 < − log 5 m 4 − m 2 + 1 < 1 ⇔ − 1 < log 5 m 4 − m 2 + 1 < 0
⇔ 1 5 < m 4 − m 2 + 1 < 1 ⇔ m 4 − m 2 + 1 < 1
( do m 4 − m 2 + 1 ≥ 3 4 > 1 5 )
⇔ m 4 − m 2 < 0 ⇔ m 2 m 2 − 1 < 0 ⇔ m ≠ 0 m 2 − 1 < 0 ⇔ m ≠ 0 − 1 < m < 1
⇔ m ∈ − 1 ; 0 ∪ 0 ; 1
Vậy S = − 1 ; 0 ∪ 0 ; 1 , tức là S là hợp của hai khoảng với nhau. Vậy D là đáp án đúng.

Đáp án C
Với f x > 0 , ∀ x ∈ ℝ . Xét biểu thức f ' x f x = 2 - 2 x *
Lấy nguyên hàm 2 vế (*), ta được ∫ d f x f x = ∫ 2 - 2 x d x
⇔ ∫ d f x f x = - x 2 + 2 x + C ⇔ ln f x = - x 2 + 2 x + C
Mà f(0) =1 suy ra C = lnf(0) = ln1 = 0. Do đó f x = e - x 2 + 2 x
Xét hàm số f x = e - x 2 + 2 x trên - ∞ ; + ∞ , có f ' x = - 2 x + 2 = 0 ⇔ x = 1
Tính giá trị f 1 = e ; lim x → - ∞ f x = 0 ; lim x → - ∞ f x = 0
Suy ra để phương trình f(x) = m có hai nghiệm thực phân biệt ⇔ 0 < m < e .

Đáp án A
Ta có 9 x + 2 x − m 3 x + 2 x − 2 m − 1 = 0 ⇔ 3 2 x + 3 x + 2 x − m 3 x − 3 x − 1 = 0
⇔ 3 x + 1 3 x + 2 x − 2 m − 1 = 0 ⇔ 3 x + 2 x − 2 m − 1 = 0
⇔ 3 x + 2 x = 2 m + 1 (*)
Xét hàm số f x = 3 x + 2 x có f ' x = 3 x . ln 3 + 2 > 0 với mọi x ∈ ℝ .
Suy ra hàm số luôn đồng biến trên R .
Để (*) có nghiệm dương thì ta phải có 2 m + 1 > f 0 = 1 ⇔ m > 0 .
Vậy T là một khoảng. Ta chọn A.

Lời giải:
Để pt có 2 nghiệm pb thì:
$\Delta'=1-(2-m)=m-1>0\Leftrightarrow m>1$
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=2\\ x_1x_2=2-m\end{matrix}\right.\)
Khi đó:
$2x_1^3+(m+2)x_2^2=5$
$\Leftrightarrow 2x_1^3+(2x_1+2x_2-x_1x_2)x_2^2=5$
$\Leftrightarrow 2(x_1^3+x_2^3)+x_1(2-x_2)x_2^2=5$
\(\Leftrightarrow 2[(x_1+x_2)^3-3x_1x_2(x_1+x_2)]+x_1^2x_2^2=5\)
\(\Leftrightarrow 2[8-6(2-m)]+(2-m)^2=5\)
\(\Leftrightarrow m^2+8m-9=0\Leftrightarrow (m-1)(m+9)=0\)
Vì $m>1$ nên không có giá trị nào của $m$ thỏa mãn.
Chọn D.
Phương trình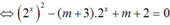
Ta thấy 1 - (m + 3) + m + 2 = 0 nên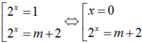
Từ đó 2x = m + 2 cần phải có nghiệm thực khác 0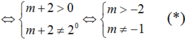
Khi đó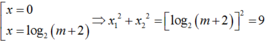
Kết hợp với m > 0 đề bài cho thì ta được m = 6 thỏa mãn.