Chọn A.

Bất phương trình ( m 2  + m + 1)x - 5m ≥ ( m 2  + 2)x - 3m - 1 ⇔ (m - 1)x ≥ 2m - 1 vô nghiệm khi

Chọn B

Phương trình vô nghiệm khi Δ' < 0

A

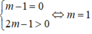
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-1=0\\m^2-2m-3\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\pm1\\m\ne-1;m\ne3\end{matrix}\right.\Leftrightarrow m=1\)

Chọn A

Câu 2 bạn ghi thiếu đề

Câu 1:

\(\Leftrightarrow\left(m^2-3m\right)x+2x< 2-m\)

\(\Leftrightarrow\left(m^2-3m+2\right)x< 2-m\)

BPT đã cho vô nghiệm khi và chỉ khi:

\(\left\{{}\begin{matrix}m^2-3m+2=0\\2-m\le0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=1\\m=2\end{matrix}\right.\\m\ge2\end{matrix}\right.\) \(\Rightarrow m=2\)

Chọn D.

+) (m + 2)x ≤ m + 1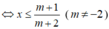 

+) 3m(x - 1) ≤ -x - 1 ⇔ 3mx - 3m + x + 1 ≤ (3m + 1)x ≤ 3m - 1

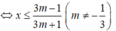
Hai bất phương trình (m + 2)x ≤ m + 1 và 3m(x - 1) ≤ -x - 1 tương đương khi và chỉ khi hai bất phương trình có cùng tập nghiệm khi đó:

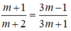
⇔ (m + 1)(3m + 1) = (m + 2)(3m - 1)

⇔ 3 m 2  + m + 3m + 1 = 3 m 2  - m + 6m - 2

⇔ 3 m 2  + m + 3m + 1 - 3 m 2  + m - 6m + 2 = 0

⇔ -m + 3 = 0

⇔ m = 3 (thỏa mãn)

Chọn B.

Xét bất phương trình:

m 2 x + m - 1 < x ⇔  m 2 x - x + m - 1 < 0 ⇔ ( m 2  - 1)x < 1 - m (1)

Với m = 1, bất phương trình (1) trở thành: 0x < 0 ⇔ 0 < 0 (Vô lý) ⇒ Bất phương trình vô nghiệm.

Với m = -1 , bất phương trình (1) trở thành: 0x < 2 ⇔ 0 < 2 (luôn đúng) ⇒ Bất phương trình có vô số nghiệm.

Vậy bất phương trình  m 2 x + m - 1 < x vô nghiệm khi m = 1.