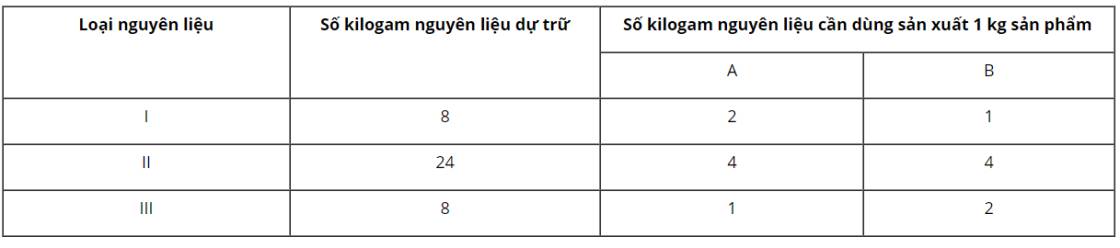
Một công ty kinh doanh nghiên cứu thị trường trước khi tung ra sản phẩm và nhận thấy để sản xuất ra một đơn vị sản phẩm loại A và B thì mất lần lượt là 2000 USD và 4000USD. Nếu sản xuất được x sản phẩm loại A và y sản phẩm loại B thì lợi nhuận mà công ty thu được là L ( x ; y ) = 8000 x 1 3 y 1 2 USD. Giả sử chi phí để sản xuất hai loại sản phẩm A ; B là 40 000USD. Gọi x0 ; y0 lần lượt là số phẩm loại A ; B để lợi nhuận lớn nhất. Tính x 0 2 + y 0 2
A.100
B. 8288.
C. 3637
D. 17319

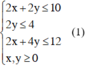

Chọn A.
Gọi x; y lần lượt là số phẩm loại A; B.
Theo đề bài ta có: 2000x + 4000y = 40 000 hay x + 2y = 20
Suy ra: x = 20 - 2y.
Ta có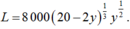
Xét hàm
Tập xác định D = (0; 10).
Nhận xét: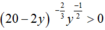 nên dấu của y’ là dấu của biểu thức
nên dấu của y’ là dấu của biểu thức 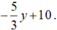
Do đó hàm số đạt giá trị lớn nhất khi y = 6 và x = 8
Vậy