Viết tiếp vào chỗ chấm:
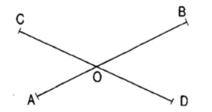
a) Đoạn thẳng AB cắt đoạn thẳng CD tại điểm ....
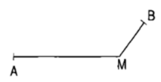
b) Đoạn thẳng AM cắt đoạn thẳng MB tại điểm ....
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp giải:
- Dùng bút chì và thước kẻ, nối hai điểm A và B; C và D.
- Tìm giao điểm của hai đoạn thẳng; đặt tên rồi điền vào chỗ trống.
Lời giải chi tiết:
a) Vẽ đoạn thẳng AB và đoạn thẳng CD.
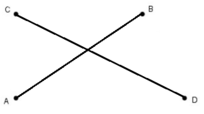
b) Đoạn thẳng AB cắt đoạn thẳng CD tại điểm

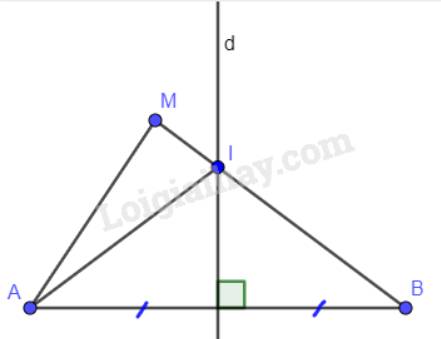
a) Ta có: Đường thẳng d là đường trung trực của đoạn thẳng AB. Mà điểm I thuộc đường thẳng d nên suy ra: IA = IB. (Một điểm thuộc đường trung trực thì cách đều hai đầu mút).
Ta có: \(MB = MI + IB\) mà IA = IB nên \(MB = MI + IA = AI + IM\).
b) Xét tam giác AMI có: \(MA < AI + IM\)(Tổng hai cạnh bất kì trong một tam giác luôn lớn hơn độ dài cạnh còn lại) mà \(MB = AI + IM\).
Vậy \(MA < MB\).

Vẽ hình 38:
+ Vẽ hai đường thẳng bất kì trên trang giấy rồi trên mỗi đường thẳng lấy ba điểm. Đặt tên các điểm là A, B, C, D, E, F như trên hình vẽ (Lưu ý: Các bạn viết tên các điểm ở phía ngoài hai đường thẳng để tránh sau đó vẽ các đoạn thẳng sẽ chèn vào tên điểm, hình không đẹp).
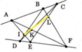
+ Vẽ các đoạn thẳng AE, BD cắt nhau tại I.
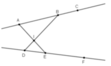
+ Vẽ các đoạn thẳng AF, CD cắt nhau tại K
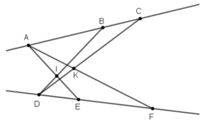
+ Vẽ các đoạn thẳng BF, CE cắt nhau tại L.
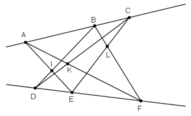
* Kiểm tra I, K, L có thẳng hàng hay không, ta vẽ đường thẳng đi qua I và K rồi xem đường thẳng đó có đi qua L hay không.
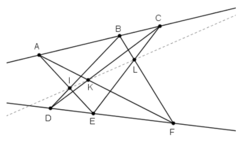
Nhận thấy I, K, L thẳng hàng.

a) Xét ΔAMC và ΔDMB có
\(\widehat{ACM}=\widehat{DBM}\)(hai góc so le trong, AC//BD)
MC=MB(M là trung điểm của BC)
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
Do đó: ΔAMC=ΔDMB(g-c-g)
b) Ta có: ΔAMC=ΔDMB(cmt)
nên AC=DB(hai cạnh tương ứng)
mà AB=AC(ΔABC cân tại A)
nên AB=BD
Phương pháp giải:
Quan sát hình ảnh, tìm hai đoạn thẳng cắt nhau tại điểm nào rồi điền tên điểm vào chỗ trống.
Lời giải chi tiết:
a) Đoạn thẳng AB cắt đoạn thẳng CD tại điểm O.
b) Đoạn thẳng AM cắt đoạn thẳng MB tại điểm M.