Chọn A

A

Đáp án: A

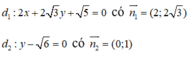
Gọi α là góc giữa hai đường thẳng d1, d2

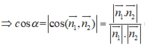
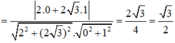
⇒ α = 30 °

ĐÁP ÁN B

Đường thẳng qua A và tạo với d1d2 các góc bằng nhau khi vuông góc với phân giác của góc tạo bởi d1d2.

Do vậy số lượng đường thẳng cần tìm là 2.

b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)

hay \(-x-4=3x+2\)

\(\Leftrightarrow-x-4-3x-2=0\)

\(\Leftrightarrow-4x-6=0\)

\(\Leftrightarrow-4x=6\)

hay \(x=-\dfrac{3}{2}\)

Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được: 

\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)

Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)

c) Vì (D2) song song với (D) nên a=-1

hay (D2): y=-x+b

Vì (D2) đi qua điểm B(-2;5)

nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được: 

-(-2)+b=5

hay b=5-2=3

Vậy: (D2): y=-x+3

b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)

hay \(-x-4=3x+2\)

\(\Leftrightarrow-x-4-3x-2=0\)

\(\Leftrightarrow-4x-6=0\)

\(\Leftrightarrow-4x=6\)

hay \(x=-\dfrac{3}{2}\)

Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được: 

\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)

Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)

c) Vì (D2) song song với (D) nên a=-1

hay (D2): y=-x+b

Vì (D2) đi qua điểm B(-2;5)

nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được: 

-(-2)+b=5

hay b=5-2=3

Vậy: (D2): y=-x+3

Ta có d 2 : 3 x − 2 y + 1 = 0   ⇔ 6 x − 4 y + 2 = 0  

Ta có điểm A(-1; 1) thuộc đường thẳng d2,.

Vì hai đường thẳng d1 và d2 song song với nhau nên ta có:

d ( d 1 ;    d 2 ) = d ( A ;    d 1 ) =    6. ( − 1 )   − 4. ( − 1 ) + 5 6 2 + ( − 4 ) 2 =   3 52

ĐÁP ÁN D