Cho tam giác ABC có trọng tâm G và trung tuyến AM. Khẳng định nào sau đây là đúng?
A. G A → = 2 G M →
B. 3 M A → + M B → + M C → = M G →
C. G A → + G B → + 2 G C → = 0 →
D. A M → = - 3 M G →
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tam giác ABC có AM và BN là hai đường trung tuyến cắt nhau tại G. Khẳng định nào sau đây đúng? (có thể chọn nhiều đáp án) *
Điểm G cách đều ba đỉnh của tam giác
Điểm G gọi là trọng tâm của tam giác
GA = 2.GM
Điểm G cách đỉnh B một khoảng bằng 2/3 độ dài đường trung tuyến BN
GA = GB
GN = 3.BN


+ Vì G là trọng tâm của tam giác ABC có AD là một trung tuyến nên AG = 2/3AD, suy ra G không thể là trung điểm của AD => B sai
+ Vì AG = 2/3 AD => GD = 1/3 AD
Mà DM = 1/3 AD nên GD = DM
Mặt khác G thuộc tia DA, M thuộc tia đối của tia DA nên D nằm giữa M và G
Do đó D là trung điểm của MG, nên A đúng.


Vì `G` là trọng tâm của tam giác
`@` Theo tính chất của trọng tâm (cách đỉnh `2/3,` cách đáy `1/3`)
`-> GA = 2GM, GA= 2/3 AM`
Xét các đáp án trên `-> D.`

+ G là trọng tâm của tam giác DEF với đường trung tuyến DH.
Theo tính chất đường trung tuyến
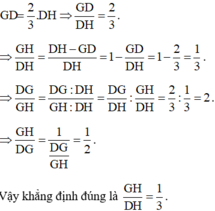

Nếu G là trong tâm tam giác ABC thì
G A → + G B → + G C → = 0 → ⇔ A G → + B G → + C G → = 0 → ⇔ A G → + B G → + C G → = 0 → = 0
Đáp án C
Do G là trọng tâm tam giác và trung tuyến AM nên AM = 3GM.
Suy ra: A M → = - 3 M G →
Đáp án D