Đáp án A

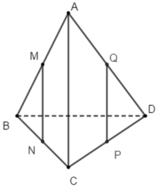
Ta có:  M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC
suy ra: MN// AC  và   M N =    1 2 A C    (1)

Tương tự:  QP là đường trung  bình của tam giác ACD nên QP // AC và Q P =    1 2 A C  (2)

Từ  (1) và (2) suy ra: tứ giác  MNPQ là hình bình hành (có các cạnh đối song song và bằng nhau)

Đáp án C

Ta có M là trung điểm AB, N là trung điểm BC

\(\Rightarrow\) MN là đường trung bình tam giác ABC

\(\Rightarrow\overrightarrow{MN}=\dfrac{1}{2}\overrightarrow{AC}\)

Hoàn toàn tương tự, PQ là đường trung bình tam giác ACD

\(\Rightarrow\overrightarrow{QP}=\dfrac{1}{2}\overrightarrow{AC}\)

\(\Rightarrow\overrightarrow{MN}=\overrightarrow{QP}\)

Ta có :M, N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC=>MN //AC vàMN = 1/2 AC (1).

Cmtt ta có:QP là đường trung bình của tam giác ADC suy ra QP//AC và QP =1/2 AC (2).

Từ (1)và(2) suy ra:

MN//QP và MN = QP

=>tứ giác MNPQ là hìnhbình hành

=>vectoMN=vectoQP

Điểm I là điểm nào thế bạn?

Phương án A sai vì : Ba đường thẳng AB, MN, CA cùng trong mặt phẳng (ABC) nên ba vecto  A B → ,   M N → ,   C A →  đồng phẳng

Phương án B sai vì: hai đường thẳng BC, AD cùng song song với mặt phẳng (MNPQ) có chứa đường thẳng MP nên ba vecto  M P → ,   B C → ,   A D →  đồng phẳng

Phương án C sai vì : Đường thẳng AD // (MNPQ) và mặt phẳng này chứa hai đường thẳng MP, PQ nên ba vecto  A D → ,   M P → ,   P Q →  đồng phẳng

Phương án D đúng vì : Đường thẳng BD cắt mặt phẳng (MNPQ) và nó chứa hai đường thẳng MP, PQ nên  M P → ,   P Q → ,   P D →  không đồng phẳng

Đáp án D

Xét hình thang ADCB có

Q,P lần lượt là trung điểm của AB,DC

=>QP là đường trung bình của hình thang ADCB

=>QP//AD//BC và \(QP=\dfrac{AD+BC}{2}=\dfrac{\dfrac{BC}{2}+BC}{2}=\dfrac{3}{4}BC\)

Ta có: M là trung điểm của BC

=>\(BM=MC=\dfrac{BC}{2}\)

Ta có: N là trung điểm của MC

=>\(MN=NC=\dfrac{MC}{2}=\dfrac{BC}{4}\)

BM+MN=BN

=>\(BN=\dfrac{1}{4}BC+\dfrac{1}{2}BC=\dfrac{3}{4}BC\)

=>QP=BN

Ta có: QP//BN

QP=BN

Do đó: \(\overrightarrow{QP}=\overrightarrow{BN}\)

=>Điểm E trùng với điểm P

Answer:

Hình bạn tự vẽ.

a, Ta xét tam giác ABC

\(AM=MB=\frac{1}{2}AB\)

\(BN=NC=\frac{1}{2}BC\)

\(\Rightarrow MN\) là đường trung bình của tam giác ABC

\(\Rightarrow\hept{\begin{cases}MN=\frac{1}{2}BC\\MN//AC\end{cases}}\)

Chứng minh tương tự, ta được

\(NP;PQ;QM\) lần lượt là đường trung bình của tam giác BCD; tam giác ACD; tam giác ABD

Ý này nếu trình bày trong vở viết bạn gộp tất cả vào một cái ngoặc "và" nhé.

\(NP=\frac{1}{2}BD\)

\(NP//BD\)

\(PQ=\frac{1}{2}AC\)

\(PQ//AC\)

\(QM=\frac{1}{2}BD\)

\(QM//BD\)

Do vậy: \(\hept{\begin{cases}MN//PQ;MN=PQ\\NP//QM;NP=QM\end{cases}}\)

Vậy MNPQ là hình bình hành

b, MNPQ là hình chữ nhật

\(\Rightarrow\widehat{MNP}=90^o\)

\(\Rightarrow MN\perp NP\)

Mà \(\hept{\begin{cases}MN//AC\\NP//BD\end{cases}}\Rightarrow AC\perp BD\)

Vậy tứ giác ABCD có hai đường chéo vuông góc thì MNPQ là hình chữ nhật