Một hình trụ có độ dài đường cao gấp đôi đường kính đáy. Biết thể tích của hình trụ là 128π c m 3 . Tính diện tích xung quanh của hình trụ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Diện tích toàn phần gấp đôi diện tích xung quanh nên:
2πRh + 2π R 2 = 2.2π R 2 => 2πRh = 2π R 2 => R = h
Vậy chiều cao của hình trụ là 3cm

Đường cao: 3 x 2 = 6(cm)
a, Diện tích xung quanh hình trụ:
\(S_{xq}=2\pi rh=2.\pi.3.6=36\pi\left(cm^2\right)\)
b, Diện tích toàn phần hình trụ:
\(S_{tp}=2.S_{đáy}+S_{xq}=2.\pi r^2+36\pi=2\pi.3^2+36\pi=54\pi\left(cm^2\right)\)
c, Thể tích hình trụ:
\(V=\pi r^2.h=\pi.3^2.6=54\pi\left(cm^3\right)\)

Lời giải:
Khái niệm đường sinh quen thuộc trong hình nón.
Như đề của bạn thì đường sinh chính là đường cao? Thế thì thể tích hình trụ: $\pi r^2h=\pi 3^2.2=18\pi$ (cm khối)
Nhưng mà diện tích xung quanh thì là: $2\pi rh=12\pi$ (cm vuông)
Thể tích và diện tích so sánh với nhau sao được?

a: Chu vi đường tròn đáy là 192/24=8cm
R=8:2:3,14=1,27(cm)
b:V=24*1,27^2*3,14=121,55(cm3)

Đáp án A
Ta có p = 2 πr = 2 π cm
Diện tích của mặt bên là diện tích của hình chữ nhật có chiều dài bằng chu vi hình tròn đáy và chiều rộng bằng chiều cao hình trụ.
S = 6 . 4 π = 24 π Chọn phương án A.

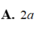
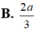
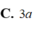
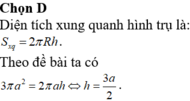

Vì h = 2R nên V = π R 2 h = π R 2 .2R=2π R 3
Mặt khác: V = 128π => R = 4cm
=> h = 8cm, Sxq = 2πRh = 64π c m 2