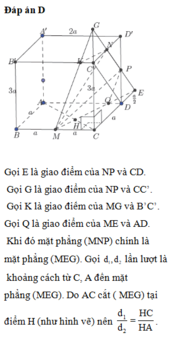
Đáp án D

Gọi E là giao điểm của NP và CD. Gọi G là giao điểm của NP và CC’. Gọi K là giao điểm của MG và B’C’. Gọi Q là giao điểm của ME và AD. Khi đó mặt phẳng (MNP) chính là mặt phẳng (MEG). Gọi d 1 ,   d 2  lần lượt là khoảng cách từ C, A đến mặt phẳng (MEG). Do AC cắt (MEG) tại điểm H (như hình vẽ) nên d 1 d 2 = H C H A . Do tứ diện CMEG là tứ diện vuông tại C nên

1 d 1 2 = 1 C M 2 + 1 C E 2 + 1 C G 2

Ta có G C ' G C = C ' N C E = 1 3  

Suy ra G C = 3 2 C C ' = 9 a 2  

Như vậy: 1 d 1 2 = 1 a 2 + 4 9 a 2 + 4 81 a 2  

Từ đó d 1 2 = 81 a 2 12 ⇒ d 1 = 9 11 . Ta có Q D M C = E D E C = 1 3 ⇒ Q D = a 3  

Ta có Δ H C M đồng dạng với Δ H A Q  nên:

H C H A = M C A Q = a 2 a − a 3 = 3 5 ⇒ d 1 d 2 = 3 5 ⇒ d 2 = 5 3 d 1 = 5.9 a 3.11 = 15 a 11

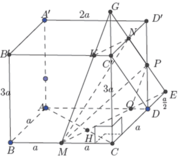
Đáp án D

Chọn hệ trục tọa độ với

  B 0 ; 0 ; 0 ; M 0 ; a ; 0 ; P a ; 2 a ; 3 a 2    v à    N a 2 ; 2 a ; 3 a

Khi đó: M P → a ; a ; 3 a 2 ;   M N → a 2 ; a ; 3 a

Do đó   n M N P = → M P → ; M N → = a 2 3 2 ; − 9 4 ; 1 2

Suy ra

M N P :   6 x − 9 y + 2 z + 9 a = 0 ;    A a ; 0 ; 0 .

Khi đó   d A ;   M N P = 6 a + 9 a 6 2 + 9 2 + 2 2 = 15 a 11 .

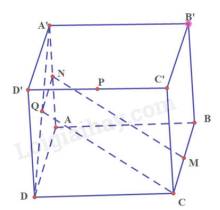
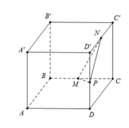
a) Ta có: N là trung điểm của AA’ nên \(\frac{{AN}}{{AA'}} = \frac{1}{2}\)

Q là trung điểm của AD’ nên \(\frac{{AQ}}{{AD'}} = \frac{1}{2}\)

Theo định lý Ta – let, ta có NQ // A’D’

Suy ra \(\frac{{NQ}}{{A'D'}} = \frac{{AN}}{{AA'}} = \frac{1}{2}\) nên\(NQ = \frac{1}{2}A'D'\)

b) Ta có: NQ // A’D’ mà A’D’ // BC nên NQ // BC hay NQ // MC (1)

Ta có \(NQ = \frac{1}{2}A'D'\) mà A’D’ = BC, \(MC = \frac{1}{2}BC\), nên NQ = MC (2)

Từ (1) và (2) suy ra MNQC là hình bình hành

c) Ta có: MNQC là hình bình hành nên MN // CQ

Mà CQ thuộc (ACD’)

Nên MN // (ACD’)

d) Gọi O là trung điểm của AC

Tam giác ACB có: O, M là trung điểm của AC, BC

Suy ra: OM // AB nên \(OM = \frac{1}{2}AB\)

Mà AB = C’D’, \(D'P = \frac{1}{2}C'D\),

Suy ra OM = D’P (1)

Ta có: OM // AB, AB // C’D’ nên OM // C’D‘ hay OM // D’P (2)

Từ (1) và (2) suy ra OMPD’ là hình bình hành. Do đó: MP // OD’

Mà OD’ thuộc (ACD’)

Suy ra: MP // (ACD’)

Mà MN thuộc (ACD’)

Do đó: (MNP) // (ACD’)

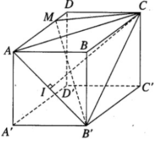
Gọi h là khoảng cách từ M đến mặt phẳng (AB’C)

Khi đó

Vì AC 2 = B ' C 2 = 5 a 2  nên tam giác ACB’ cân tại C. Do đó, đường trung tuyến CI của tam giác ACB’ cũng là đường cao.

Ta có:

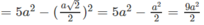
Do đó

Từ đó suy ra

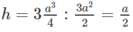
ta có : 

\(V_{M.AB'C}=V_{B'.MAC}=\frac{B'B.S_{ABC}}{3}\)

Mà BB'=A'A=a

\(S_{AMC}=\frac{CD.AM}{2}=\frac{a.2a}{2.3}=\frac{a^2}{3}\)

=> \(V_{M.AB'C}=\frac{a^3}{9}\) (1)

=> d_M,(AB'C)=\(\frac{3.V_{M.AB'C}}{S_{AB'C}}\)  (2)

tam giác AB'C cps \(AB=B'C=2\sqrt{3}\)

và \(AB=a\sqrt{2}\)

=>\(S_{AB'C}=\frac{a^2\sqrt{5}}{2}\)                    (3)

Từ (1), (2)&(3)

=> d_{M;(AB'C)=\(\frac{2a}{3\sqrt{a}}\)}

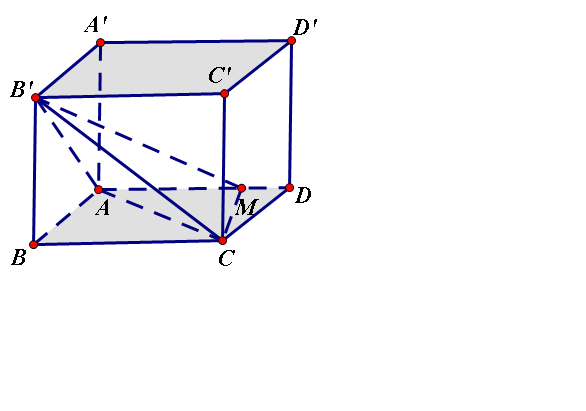
Pytago tính đuợc 3 cạnh $\Delta AMC$

$\mathrm{\backslash (AC=a\backslash sqrt\{5\}\backslash )}\sqrt{\mathrm{;}}$$\backslash (AM=\backslash frac\{3a\}\{2\}\backslash )$,         \(MC=\frac{a\sqrt{5}}{2}\)

Dùng công thức $Heron$

\(V_{M.AB'C}=V_{B.AB'C}=\frac{a^3}{4}\)

Mặt khác dùng công thức $Heron$ cũng tính được \(S_{AB'C}=\frac{3a^2}{2}\)

=> \(d_{\left(M;\left(AB'C\right)\right)}=\frac{3V_{M.AB'C}}{S_{AB'C}}=\frac{a}{2}\)

Đáp án A

Giả sử AB = x

Đáp án A

Chọn hệ trục tọa độ như hình vẽ

Đáp án A

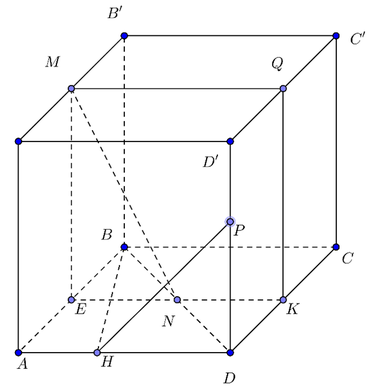
Qua N vẽ EK song song với A D E ∈ A B , K ∈ D C .

Qua M vẽ MQ song song với  A ' D ' Q ∈ D ' C '

Ta có A A ' D ' D / / E M Q K ,mà H P ⊂ A A ' D ' D , M N ⊂ E M Q K  nên

d M N , H P = d A A ' D ' D , E M Q K = 1 2 d A ' A D D ' , B ' B C C ' = 1 2 B H = 1 2 a 3 2 = a 3 4 .