Mỗi khẳng định sau đúng hay sai? Vì sao?
(4 - √3).2x < √3(4 - √13) ⇔ 2x < √13
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 4 2017
a) Đúng, v ì √ 0 , 0001 = √ 0 , 01 2 = 0 , 01
b) Sai, vì vế phải không có nghĩa.
(Lưu ý: √A có nghĩa khi A ≥ 0)
c) Đúng, v ì 7 = √ 7 2 = √ 49 > √ 39
6 = √ 6 2 = √ 36 < √ 39
d) Đúng, v ì 4 - √ 13 = √ 4 2 - √ 13 = √ 16 - √ 13 > 0
Do đó: (4 - √13).2x < √3(4 - √13) (giản ước hai vế với (4 - √13))
⇔ 2x < √3
23 tháng 4 2021
a) Đúng. Vì √0,0001=√0,012=0,010,0001=0,012=0,01
Vì VP=√0,0001=√0,012=0,01=VTVP=0,0001=0,012=0,01=VT.
b) Sai.
Vì vế phải không có nghĩa do số âm không có căn bậc hai.
c) Đúng.
Vì: 36<39<4936<39<49 ⇔√36<√39<√49⇔36<39<49
⇔√62<√39<√72⇔62<39<72
⇔6<√39<7⇔6<39<7
Hay √39>639>6 và √39<739<7.
d) Đúng.
Xét bất phương trình đề cho:
(4−√13).2x<√3.(4−√13)(4−13).2x<3.(4−13) (1)(1)
Ta có:
16>13⇔√16>√1316>13⇔16>13
⇔√42>√13⇔42>13
⇔4>√13⇔4>13
⇔4−√13>0⇔4−13>0
Chia cả hai vế của bất đẳng thức (1)(1) cho số dương (4−√13)(4−13), ta được:
(4−√13).2x(4−√13)<√3.(4−√13)(4−√13)(4−13).2x(4−13)<3.(4−13)(4−13)
⇔2x<√3.⇔2x<3.
Vậy phép biến đổi tương đương trong câu d là đúng.
CM
24 tháng 9 2017
a) Khẳng định đúng. b) Khẳng định đúng.
c) Khẳng định đúng. d) Khẳng định sai.
CM
26 tháng 2 2017
Khẳng định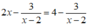 
và 2x = 4 là hai phương trình tương đương là sai.
Vì phương trình 2x = 4 có nghiệm x = 2. Nhưng với x = 2 thì phân thức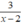 
vô nghĩa.
Vậy x = 2 không là nghiệm của phương trình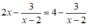 
.
CM
5 tháng 5 2019
(Kí hiệu: VP = vế phải; VT = vế trái)
a) Ta có: (-2) + 3 = 1
Vì 1 < 2 nên (-2) + 3 < 2.
Do đó khẳng định (-2) + 3 ≥ 2 là sai.
b) Ta có: 2.(-3) = -6
⇒ Khẳng định -6 ≤ 2.(-3) là đúng.
c) Ta có: 4 + (-8) = -4
15 + (-8) = 7
Vì -4 < 7 nên 4 + (-8) < 15 + (-8)
Do đó khẳng định c) đúng
d) Với mọi số thực x ta có: x2 ≥ 0
⇒ x2 + 1 ≥ 1
⇒ Khẳng định d) đúng với mọi số thực x.
Đúng, vì 4 - √13 = √42 - √13 = √16 - √13 > 0
Do đó: (4 - √13).2x < √3(4 - √13) (giản ước hai vế với (4 - √13))
⇔ 2x < √3