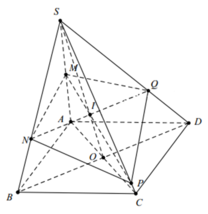
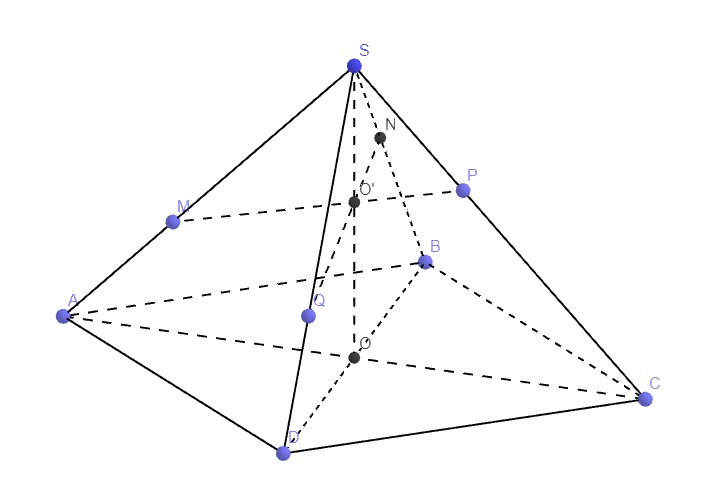
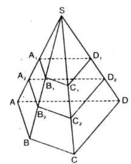
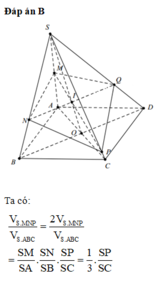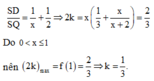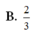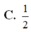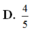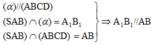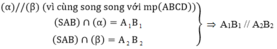Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SA, N là điểm trên đoạn SB sao cho SN = 2NB. Mặt phẳng chứa MN cắt đoạn SD tại Q và cắt đoạn SC tại P. Tỉ số V S . M N P Q V S . A B C D lớn nhất bằng
A. 2 5
B. 1 3
C. 1 4
D. 3 8