Đáp án là C.

Ta có: đồ thị hàm số  f ' x    cắt trục  tại  4 điểm phân biệt tức phương trình f ' x = 0  có 4  nghiệm phân biệt. Tuy nhiên, nhìn vào đồ thị ta thấy dấu của f ' x  chỉ đổi khi qua  nghiệm đầu. Vậy hàm số f ' x  có  3 cực trị.

Đáp án D.

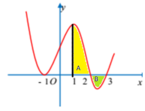
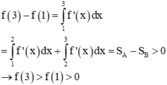
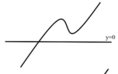
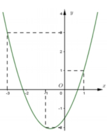
Đồ thị hàm số y = f(x) có dạng:

Đồ thị hàm số y = |f(x)| có dạng:

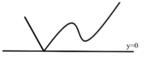
→ Hàm số y = |f(x)| có 3 điểm cực trị.

Chọn A

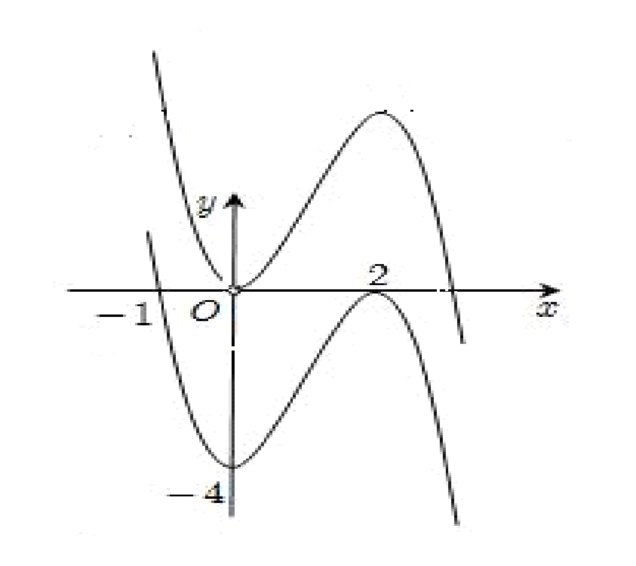
Ta có: có đồ thị là phép tịnh tiến đồ thị hàm số y= f’(x)  theo phương Oy lên trên 4 đơn vị.

Khi đó đồ thị hàm số y= f( x) + 4x  cắt trục hoành tại 1 điểm.

 ta chọn đáp án A.

Đáp án A.

Phương pháp: Tính g’(x) tìm các nghiệm của phương trình g’(x) = 0

Điểm x₀ được gọi là điểm cực tiểu của hàm số y = g(x) khi và chỉ khi g’(x₀) = 0  và qua điểm x = x₀ thì g’(x) đổi dấu từ âm sang dương.

Cách giải:

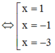
Khi x<1 ta có: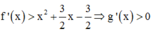 

Khi x>1 ta có: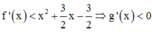 

Qua x = 1, g’(x) đổi dấu từ dương sang âm => x = 1 là điểm cực đại của đồ thị hàm số y = g(x)

Chứng minh tương tự  ta được x = –1 là điểm cực tiểu và x = –3 là điểm cực đại của đồ  thị  hàm số y = g(x)

Đáp án C

Ta có f ' x = 0 ⇔ x = 1 ; 2 ; 3 ⇒  hàm số có 3 điểm cực trị

Lại có g x = f x - m - 2018 ⇒ g ' x = f ' x = 0 ⇒  có 3 nghiệm phân biệt

Suy ra phương trình f x = m + 2018  có nhiều nhất 4 nghiệm

Xét  y = f x + 1 ⇒ y ' = f ' x + 1 < 0 ⇔ [ x + 1 ∈ 1 ; 2 x + 1 ∈ 3 ; + ∞ ⇔ [ 0 < x < 1 x > 2

Suy ra hàm số y = f(x + 1) nghịch biến trên khoảng (0;1).

Đáp án B

Phương pháp: Từ đồ thị hàm số y = f’(x) lập BBT của đồ thị hàm số y = f(x) và kết luận.

Cách giải: Ta có 

BBT:

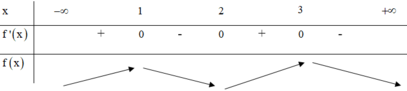
Từ BBT ta thấy (I) đúng, (II) sai.

Với  => Hàm số y = f(x+1) nghịch biến trên khoảng (0;1).

=>(III) đúng.

Vậy có hai khẳng định đúng