Đáp án là A

Chọn C

Ta có  y ' = 3 x 2 - 6 m x + 3 ( m 2 - 1 )

Hàm số (1) có cực trị thì PT y ' = 0  có 2 nghiệm phân biệt

⇔ x 2 - 2 m x + m 2 - 1 = 0  có 2 nhiệm phân biệt

Khi đó, điểm cực đại A ( m - 1 ; 2 - 2 m ) và điểm cực tiểu  B ( m + 1 ; - 2 m )

Ta có  O A = 2 O B ⇔ m 2 + 6 m + 1 = 0

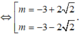
\(y=x^4-2\left(m^2-m+1\right)x+m-1\)

\(y'=4x^3-4\left(m^2-m+1\right)x\)

\(y'=0\Leftrightarrow4x^3-4\left(m^2-m+1\right)x=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=\pm\sqrt{m^2-m+1}\end{cases}}\)

Khoảng cách giữa hai điểm cực tiểu là: 

\(2\sqrt{m^2-m+1}=2\sqrt{\left(m-\frac{1}{2}\right)^2+\frac{3}{4}}\ge2\sqrt{\frac{3}{4}}\)

Dấu \(=\)khi \(m-\frac{1}{2}=0\Leftrightarrow m=\frac{1}{2}\).

Ta có 

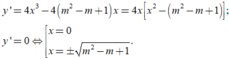
Suy ra đồ thị có hai điểm cực tiểu là  A - m 2 - m + 1 ; y C T và  B m 2 - m + 1 ; y C T

Khi đó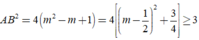 

Dấu  xảy ra khi m=1/2.

Chọn B.

Ta có : y’ = 4x³-4( m+ 1) x= 4x( x²- (m+ 1) ).

Hàm số có  điểm cực trị khi và chỉ khi y’ = 0 có  nghiệm phân biệt hay m+1> 0 suy ra m> - 1. (*)

Khi đó, ta có: 

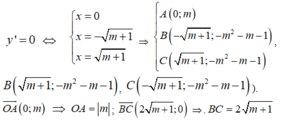
Do đó  O A = B C ⇔ m = 2 m + 1 ⇔ m 2 - 4 m - 4 = 0 ( ∆ ' = 8 ) ⇔ m = 2 ± 2 2 (thỏa mãn (*)).

Vậy  m = 2 ± 2 2 .

Chọn  A.

Chọn A

Ta có:

Hàm số có 3 điểm cực trị khi và chỉ khi :

y ' có 3 nghiệm phân biệt

⇔ m + 1 > 0 ⇔ m > - 1   ( * )

Khi đó, ta có  y ' = 0

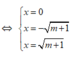
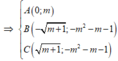
(vai trò của B, C trong bài toán là như nhau ) nên ta giả sử

Ta có: O A ( 0 ; m ) ⇒ O A = m ⇒ B C = 2 m + 1

Do đó OA = BC

⇔ m = 2 ± 2 2 ( t h ỏ a   m ã n )   ( * )

Vậy  m = 2 ± 2 2