Xét (O) có

AC là dây

BD là dây

AC//BD

Do đó: AC=BD

a: AM//BN

=>AMBN là hình thang

=>góc MAN+góc ANB=180 độ

=>góc NAM=góc AMB

=>AN//MB

mà AM//BN

nên AMBN là hình bình hành

=>BM=AD và AB cắt MN tại trung điểm của mỗi đường

=>O là trung điểm của MN

b: MD//AB

Xét ΔMDN có

góc MDN là góc nội tiếp chắn nửa đường tròn

=>góc MDN=90 độ

=>MD vuông góc DN

=>DN vuông góc AB

c: ΔODN cân tại O

mà OE là đường cao

nên E là trung điểm của DN

=>DE=EN

a: Xét (O) có

ΔACB nội tiếp

AB là đường kính

=>ΔABC vuông tại C

=>AC vuông góc CB

=>CB vuông góc BD

=>B nằm trên đường tròn đường kính CD

Xét tứ giác ACBD có

AB căt CD tại trung điểm của mỗi đường

AB=CD

=>ACBD là hình chữ nhật

=>AC=BD

b:

Th1: AC<BC

mà OM,ON lần lượt là khoảng cách từ O đến AC,BC

nên OM>ON

TH2: 

AC>BC

mà OM,ON lần lượt là khoảng cách từ O đến AC,BC

nên OM<ON

TH3: 

AC=BC

mà OM,ON lần lượt là khoảng cách từ O đến AC,BC

nên OM=ON

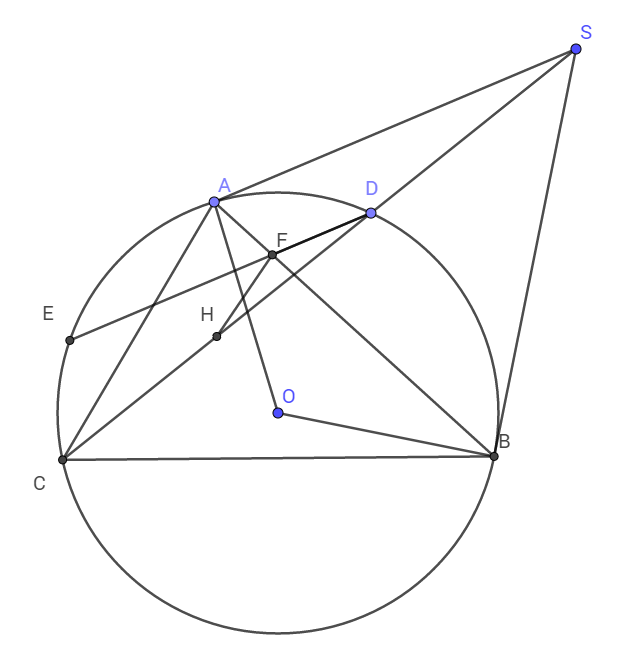
Ta có các tam giác vuông AOS; HOS, BOS có chung cạnh huyền OS nên S, A, H, O, B nội tiếp đường tròn đường kính OS.

Khi đó ta có :

\(\widehat{ASH}=\widehat{ABH}\) (Hai góc nội tiếp cùng chắn cung AH)

Mà \(\widehat{ASH}=\widehat{FDH}\)  (Hai góc đồng vị)

\(\Rightarrow\widehat{ABH}=\widehat{FDH}\)

Suy ra tứ giác HFDO nội tiếp.

Từ đó ta có \(\widehat{FHD}=\widehat{ABD}\)(Hai góc nội tiếp)

Mà \(\widehat{ABD}=\widehat{ACD}\) (Hai góc nội tiếp)

Nên \(\widehat{FHD}=\widehat{ACD}\)

Chúng lại ở vị trí đồng vị nên HF // AC.

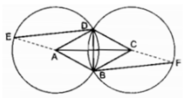
Ta có (A; AD) và (C; CB) có bán kính AD = CB là cạnh của hình thoi ABCD nên hai đường tròn đó bằng nhau.

Vì CD = CB, suy ra D thuộc (C; CB)

Vì AB = AD, suy ra B thuộc (A; AD)

Suy ra (A; AD) và (C; CB) cắt nhau tại B và D.

DE // BF (gt)